How to find the length of sides of isosceles triangle

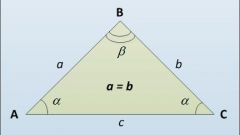
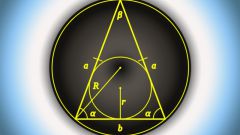
If you know the length of base of isosceles triangle (A) and the value adjacent to it angle (angle between the base and any lateral face) (α), then calculate the length of each of the sides (B) based on the spherical law of cosines. It will be equal to the private from dividing the length of the base to twice the value of the cosine of the known angle B=A/(2*cos(α)).

The length of the sides of an isosceles triangle, which is its base (A) can be calculated on the basis of the same cosines, if you know the length of its lateral side (B) and the angle between it and the base (α). It will be equal to twice the product of the known sides into the cosine of the known angle A=2*B*cos(α).

Another way to find the length of the base of an isosceles triangle can be used if we know the value of him opposite the angle (β) and the length of the lateral side (B) of the triangle. It will be equal to twice the product of length of the lateral sides by the sine of half the value of the known angle A=2*B*sin(β /2).

Similarly, we can deduce the calculation formula of lateral sides of the isosceles triangle. If the known base length (A) and the angle between the equal sides (β), the length of each (B) will be equal to the result of dividing the base length to twice the sine of half the value of the known angle B=A/(2*sin(β /2)).

If you know the radius described around an isosceles triangle on the circle (R), then the lengths of its sides can be calculated, knowing the value of one of the corners. If we know the value of the angle between the sides (β), the length of the partiesconstituting the grounds (A), is equal to twice the product of the radius of the circumscribed circle by the sine of this angle A=2*R*sin(β).

If you know the radius of the circumscribed circle (R) and the angle adjacent to the base (α), the length of the lateral side (B) will be equal to twice the product of the base length by the sine of the known angle B=2*R*sin(α).