How to find the side of a triangle, knowing two sides

If you know that the triangle is rectangular, it gives you knowledge of the value of one of the corners, i.e., missing for calculation of the third parameter. The required side (C) hypotenuse - the side lying opposite the right angle. Then to calculate, extract square root and squared and folded the lengths of the other two sides (A and B) of this figure: C=√(A2+B2). If the desired direction is the leg, remove the square root from the difference between the squares of the lengths of the longer (hypotenuse) and lower (second leg) sides: C=√(A2-B2). These formulas are derived from the Pythagorean theorem.

Knowledge as a third parameter to the perimeter of the triangle (P) reduces the problem of computing the length of a missing side (S) to a simple subtraction operation - subtract from perimeter the length of both (A and B) famous faces: C=P-A-B. This formula follows from the definition of the perimeter which is the length of the polygonal line bounding the area of the shape.

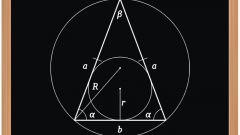
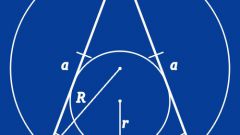
The presence of baseline angle (γ) between the sides (A and B) of known length will require to find the length of the third (C) computation of trigonometric functions. Lift both the lengths of the sides in the square and add the results. Then, from this value subtract the product of their lengths into the cosine of the known angle, and in the end remove from the obtained values of the square root: C = √(A2+B2-A*B*cos(γ)). The theorem that you used in the calculations, is called the theorem of sines.

A well-known area of the triangle (S) will require the use of three formulas. The first defines the area as half of the work length of the known sides (A and B) the sine of the angle between them. Express from it the sine of an angle and you will get the expression 2*S/(A*B). The second formula allows to Express the cosine of the same angle as the sum of the squares of the sine and cosine of the same angle equals one, the cosine is the square root of the difference between the unit and the square received the previous expression: √(1-(2*S/(A*B))2). The third formula is a theorem, the law of cosines was used in the previous step, replace in it is the cosine of the resulting expression and you will have the following formula for calculation: C = √(A2+B2-A*B*√(1-(2*S/(A*B))2)).