You will need
- The sides of the triangle, the angles of a triangle
Instruction
1
For starters, you can consider special cases and start with the case of a right triangle. If you know that the triangle is rectangular and known for one of its acute angles, then the length of one of the parties can be found and other sides of the triangle.
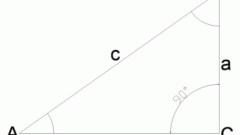
To find the length of the other sides you need to know which side of the specified triangle is the hypotenuse or any of the other two sides. The hypotenuse lies against the straight edge, the legs form a right angle.
Consider right triangle ABC with right angle ABC. Imagine you are given its hypotenuse and AC, for example, the acute angle BAC. Then the other two sides of the triangle are equal: AB = AC*cos(BAC) (adjacent side to angle BAC), BC = AC*sin(BAC) (the side opposite the angle BAC).
To find the length of the other sides you need to know which side of the specified triangle is the hypotenuse or any of the other two sides. The hypotenuse lies against the straight edge, the legs form a right angle.
Consider right triangle ABC with right angle ABC. Imagine you are given its hypotenuse and AC, for example, the acute angle BAC. Then the other two sides of the triangle are equal: AB = AC*cos(BAC) (adjacent side to angle BAC), BC = AC*sin(BAC) (the side opposite the angle BAC).
2
Let now set to the same angle BAC, for example, the side AB. Then AC is the hypotenuse of this right triangle is equal to: AC = AB/cos(BAC) (respectively, AC = BC/sin(BAC)). The other leg BC is given by BC = AB*tg(BAC).
3
Another special case - if the triangle ABC is isosceles (AB = AC). Imagine you are given the base BC. If you specify the angle BAC, then the sides AB and AC can be calculated using the following formula: AB = AC = (BC/2)/sin(BAC/2).
If you specify the base angle ABC or ACB, then AB = AC = (BC/2)/cos(ABC).
If you specify the base angle ABC or ACB, then AB = AC = (BC/2)/cos(ABC).
4
Let set one of the sides AB or AC. If you know the angle BAC, BC = 2*AB*sin(BAC/2). If you know the angle ABC or the angle ACB at the base, BC = 2*AB*cos(ABC).
5
You can now consider the General case of a triangle when length of one side and one angle is not enough to find the length of the other side.
Let in triangle ABC the side AB is set to one of the adjoining corners, for example, angle ABC. Then, knowing the side BC, by theorem of cosines to find the side AC. It will be equal to: AC = sqrt (AB^2)+(BC^2)-2*AB*BC*cos(ABC))
Let in triangle ABC the side AB is set to one of the adjoining corners, for example, angle ABC. Then, knowing the side BC, by theorem of cosines to find the side AC. It will be equal to: AC = sqrt (AB^2)+(BC^2)-2*AB*BC*cos(ABC))
6
Now let the given side AB and the opposite angle ACB to her. May also known, for example, angle ABC. By theorem of sines, AB/sin(ACB) = AC/sin(ABC). Hence, AC = AB*sin(ABC)/sin(ACB).