Instruction
1
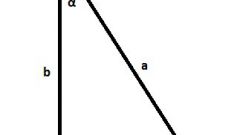
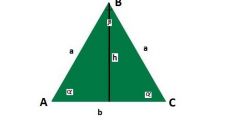
If the known values of the two angles (α and β) and the length of one side (C), the lengths of the other two sides can be determined, but the calculation formula will vary, depending on, adjacent both known angle to the side of known length. If Yes, then based on the theorem of sines and given the theorem about sum of angles in a triangle, the length of the side (A), which lies opposite the angle α, can be defined as the ratio of product of the sine of that angle on a known side length to the sine of the difference between the unfolded angle (180°) and the sum of the two known angles: A=sin(α)∗C/(sin(180°-α-β)). To determine the length of the third side (B) lying opposite the angle β, this formula should be changed accordingly: B=sin(β)∗C/(sin(180°-α-β)).
2
If a party (B) of known length is not between the two known angles (α and β), and is adjacent to only one of them (e.g. α), the calculation formula of the lengths of the remaining sides will change. Side (C), lying opposite the unknown angle will have a length determined by the ratio of the product of the sine of the angle of losses to the total value of all angles is 180°, the length of the known side to the sine of the angle lying opposite to it: C=sin(180°-α-β)∗B/sin(β). And the length of the third side (A) can be determined by this formula: A=sin(α)∗B/sin(β).
3
If you know the lengths of two sides (A and B) and the angle of one corner, then to find the length of a missing side you can use the theorem of cosines. If the angle of known value (γ) lies between the known sides, the length of the required side (C) is equal to the square root of the difference between the sum of the squares of the lengths of the known sides and twice the product of the lengths of these sides into the cosine of the known angle: C=√(A2+B2-2∗A∗B∗cos(γ)).