Instruction
1
Find the square to the 1st side. Let's build the number 15 in the square, get the 225.
2
Find square 2nd side. Let's build the number 9 in the square, get 81.
3
Add the results of the 1st and 2nd step. Add 225 to 81, get 306.
4
Calculate the square root of the result of the 3rd step. Root of the number 306 is approximately equal to 17.49 inches. This is the length of the hypotenuse.
Note
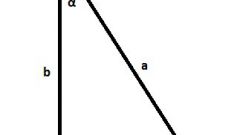
If an unknown variable is one of the shorter sides, then at the 3rd step are different. From the square of the hypotenuse subtract the square of the leg. The rest is not changing. For example, was known to the hypotenuse is 17.49 inches. Also known side is 9 cm. Find the length of the other leg.
The number of 17.49 squared is equal to 305.9. The number 9 squared is 81. Subtract from the number to 305.9 81 received 224,9. Calculated from this number the root is received 14.99 inches - the length of the second leg. It turned out a little less than 15 centimeters because of 17.49 - we initially have a rough, rounded value.
The number of 17.49 squared is equal to 305.9. The number 9 squared is 81. Subtract from the number to 305.9 81 received 224,9. Calculated from this number the root is received 14.99 inches - the length of the second leg. It turned out a little less than 15 centimeters because of 17.49 - we initially have a rough, rounded value.
Useful advice
To confidently solve problems by using the Pythagorean theorem, work out a few times. Decide on 50 different tasks with different rectangular triangles. You won't forget this theorem ever.