Instruction
1
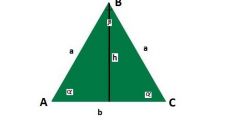
To calculate the length of the sides of an isosceles triangle (b) according to the known conditions of the length of its base (a) and the value of the adjacent angle (α) use the theorem of cosines. It implies that you should divide the length of the known sides for twice the cosine is given in terms of angle: b = a/(2*cos(α)).
2
The same theorem and apply for the reverse operation - calculate the length of the base (a) at a known length of sides (b) and value of angle (α) between these two parties. In this case, the theorem allows to obtain the equality, the right part of which contains twice the product of the lengths of the known sides into the cosine of the angle: a = 2*b*cos(α).
3
If in addition the lengths of the sides (b) in terms of the magnitude of the angle between them (β), to calculate the length of the base (a) use the theorem of sines. It implies a formula, according to which should be twice the length of the side multiplied by the sine of half of the known angle: a = 2*b*sin(β /2).
4
The theorem of sines can be used to find the length of the lateral side (b) of an isosceles triangle if the known base length (a) and opposite him the value of angle (β). In this case, double the sine of half of the known angle divided by the resulting value of the length of the base: b = a/(2*sin(β/2)).
5
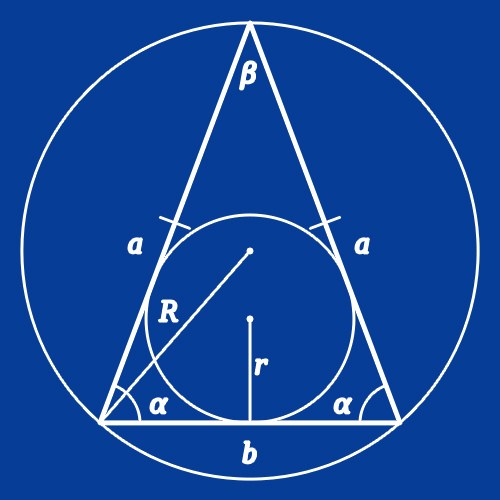
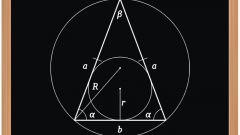
If the isosceles triangle circumscribed circle, the radius of which (R) is known, to calculate the lengths of the sides need to know the measure of the angle at one vertex of the shape. If the conditions given information about the angle between the sides (β), calculate the length of the base (a) of the polygon by doubling the product of the radius by the sine of this angle: a = 2*R*sin(β). If given the value of the base angle (α) to find the length of the lateral side (b) just replace the angle in the formula: b = 2*R*sin(α).