Instruction
1
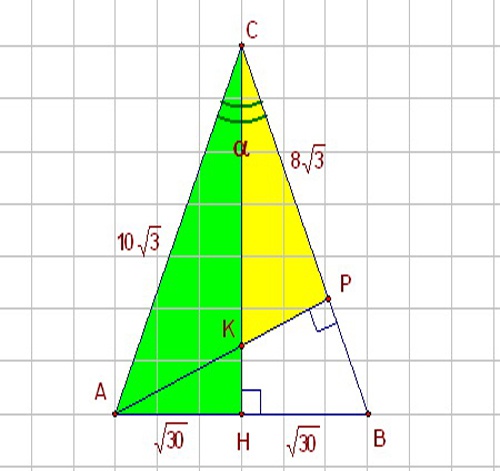
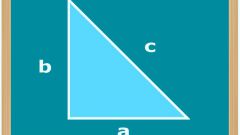
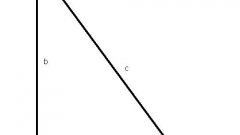
If you know one of the sides of a triangle and the angle between it and the other party, use the trigonometric functions - sineom Kosineohms. Imagine a right triangle HBC , which angle α is 60 degrees. Triangle HBC is shown in the figure. Since the sine, as you know, is the ratio of the opposite leg to the hypotenuse, andthe sine - ratio of the adjacent leg to the hypotenuse, to solve this problem, use the following relation between these parameters:sin α=NV/Sootvetstvenno, if you want to know the side of a right triangle, let's Express it using the hypotenuse as follows:HB=BC*sin α
2
If the problem, on the contrary, given side of a triangle, find the hypotenuse, according to the following ratio between the specified values:BC=HB/sin APO analogy, find the sides of the triangle and using tosineand changing the previous expression in the following way:cos α=HC/BC
3
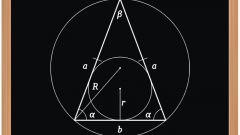
In elementary mathematics there is the concept of the theorem is the sine ofs. Guided by the facts which describes this theorem, you can also find the sides of the triangle. In addition, it allows you to find the sides of a triangle inscribed in a circle if the radius is known is known to last. Use the ratio specified below:a/sin of α=b/sin b=c/sin y=2RЭта theorem applicable in the case when given two sides and angle triangle, or given one of the angles of a triangle and the radius described around the circumference.
4
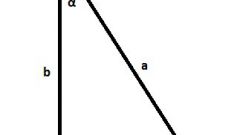
An addition theorem of the sine ofs, and exist in substantially the theorem forthe sine ofs, which, like the previous one, also applies to the triangles in all three varieties: right angle, acute and obtuse. Guided by the facts, which prove this theorem, we can find the unknown values using the following relationship:c^2=a^2+b^2-2ab*cos α