Instruction
1
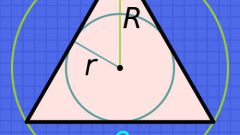
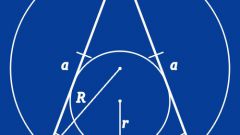
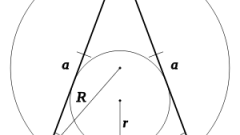
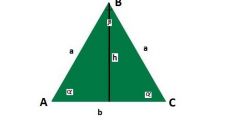
The sides of the triangle, like other polygons have their own names: the sides, base, and hypotenuse and legs of the figure with a right angle. This facilitates the calculations and formulas, making them more obvious even if the triangle is arbitrary. The figure of graphics, so it is always possible to arrange so as to make the solution of the problem more visible.
2
Sides of any triangle are connected and the other characteristics of the various ratios that help calculate the required value in one or more actions. Thus the more complex the task, the longer the sequence of steps.
3
The solution is simplified if the triangle is standard: the words "rectangular", "isosceles", "equilateral" immediately allocate a certain relationship between its sides and angles.
4
The lengths of the sides in a right triangle are connected by Pythagorean theorem: the sum of the squares of the legs equals the square of the hypotenuse. And the angles, in turn, are associated with the parties to the theorem of sines. It affirms the equality relations between the lengths of the sides and the trigonometric function sine of the opposite angle. However, this is true for any triangle.
5
Two sides of an isosceles triangle are equal. If their length is known, it is enough only one value to find the third. For example, suppose we know the height held to it. This cut divides the third side into two equal parts, and allocates two rectangular triangleH. Considered one of them, by the Pythagorean theorem find the leg and multiply it by 2. This will be the length of an unknown side.
6
Side of the triangle can be found through other sides, corners, length, altitude, median, bisector, perimeter size, area, inradius, etc. If you can't apply the same formula to produce a series of intermediate calculations.
7
Consider an example: find side of an arbitrary triangle, knowing the median ma=5, held for her, and the lengths of the other two medians mb=7 and mc=8.
8
Resented involves the use of formulas for the median. You need to find the way . Obviously, there should be three equations with three unknowns.
9
Write down the formulae for the medians:ma = 1/2•√(2•(b2 + c2) – a2) = 5;mb = 1/2•√(2•(a2 + c2) – b2) = 7;mc = 1/2•√(2•(a2 + b2) – c2) = 8.
10
Express c2 from the third equation and substitute it into the second:c2 = 256 – 2•a2 – 2•b2 b2 = 20 → c2 = 216 – a2.
11
Lift both sides of the first equation in the square and find a by entering explicit values:25 = 1/4•(2•20 + 2•(216 – a2) – a2) → a ≈ 11,1.