Instruction
1
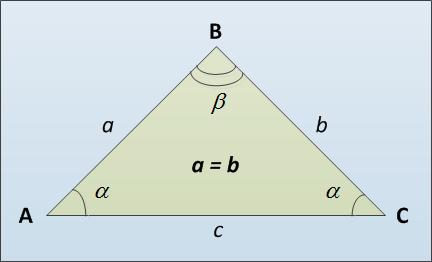
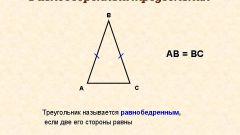
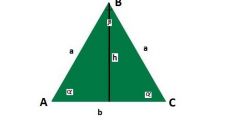
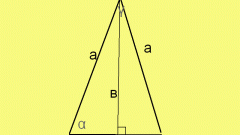
The base of the triangle is the third side of the AC (see figure), perhaps distinct from side-points of equal sides AB and BC. Here are a few ways of calculating the base length of an isosceles triangle. First, you can use the theorem of sines. It States that the sides of the triangle is directly proportional to the value of the sines of the opposite angles: a / sin α = c / sin β. How do we obtain that c = a * sin β / sin α.
2
Here is an example of the calculation of the base of the triangle by the theorem of sines. Let a = b = 5, α = 30°. Then, by the theorem about sum of angles of a triangle β = 180° - 2 * 30° = 120°. C = 5 * sin 120° / sin 30° = 5 * sin 60° / sin 30° = 5 * √3 * 2 / 2 = 5 * √3. Here to compute the value of sine of an angle β = 120° we have used the formula of the coercion, according to which sin (180° - α) = sin α.
3
The second way to find the base of the triangle – using the spherical law of cosines: the square of the sides of a triangle is equal to the sum of the squares of the other two sides minus twice the product of these sides and the cosine of the angle between them. We find that the base square c^2 = a^2 + b^2 – 2 * a * b * cos β. Then we find the length of the base c, extracting the square root of this expression.
4
Let's consider an example. Suppose we are given the same parameters as in the previous task (see paragraph 2). a = b = 5, α = 30°. β = 120°. with^2 = 25 + 25 - 2 * 25 * cos 120° = 50 - 50 * (- cos 60°) = 50 + 50 * ½ = 75. In this calculation we applied the formula of bringing to find cos 120°: cos (180° - α) = - cos α. Extracted the square root and obtain the value of c = 5 * √3.
5
Consider a special case of an isosceles triangle – an isosceles right-angled triangle. Then by the Pythagorean theorem we immediately find a basis c = √(a^2 + b^2).