How to find the sine of an angle in an equilateral triangle

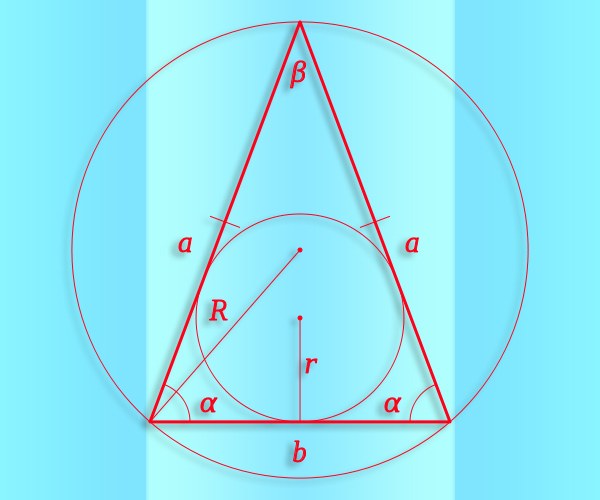
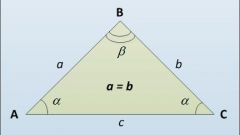
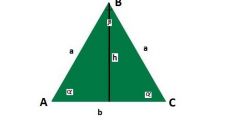
If the data is a known value of at least one angle (α) in an isosceles triangle, it will allow you to find the other two (β and γ), and hence the sine of any of them. Based on the theorem about the angle sum, which says that in the triangle it must be equal to 180°. If the angle of known value lies between the lateral sides, the magnitude of each of the other two equal half the difference between 180° and an angle are known. It means that you can use in the calculation of such an identity: sin(β) = sin(γ) = sin((180°-α)/2). If you know the angle adjacent to the base of the triangle, this identity splits into two equations: sin(β) = sin(α) and sin(γ) = sin(180°-2*α).

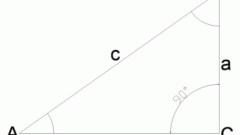
Knowing the radius (R) of the circle described around this triangle, and the length of any of the parties (for example,) without resorting to the computation of trigonometric functions to calculate the sine of the angle (α) lying opposite this side. Use the theorem of sines - from this it follows that the desired value is equal to half the ratio between the side length and radius sin(α) = ½*R/a.

Known area (S) and length side (a) of an isosceles triangle will calculate the sine of the angle (β) lying opposite the base of the figure. To do this, double the area and divide the result by the squared length of the sides: sin(β) = 2*S/a2. If in addition the lengths of the sides are known and the length of the base (b), a square can be replaced by the product of the lengths of these two sides: sin(β) = 2*S/(a*b).

If you know the lengths of the sides (a) and base (b) isosceles triangle to calculate the sineand the angle at the base (α) it is possible to even use the theorem tothe sine ofs. From this it follows that tothe sine of this angle is equal to half of the ratio of the length of the base to the length of the sides: cos(α) = ½*b/a. Sinus and cosinus connected by the equation: sin2(α) = 1-cos2(α). Therefore, to calculate the sineand extract the square root of the difference between one and a quarter ratio of the squares of the lengths of the base and the side: sin(α) = √(1-cos2(α)) = √(1-¼*b2/A2).