How to find the side of isosceles triangle if the base

Depending on the circumstances of a particular task, you can find the side of an isosceles triangleif the base and any additional element.

The base and height to it.The perpendicular drawn to the base of an isosceles triangleis the concurrent height, median and bisector of the opposite angle. This interesting feature you can use by applying the theorem of Pythagoras:a = √(h2 + (c/2)2), where a is the length of the equal sides of the triangle, h is the height drawn to the base S.

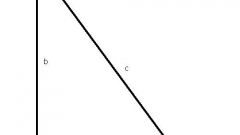
The base and the altitude to one side.Drawing an altitude to the side, you'll get a rectangular triangle. The hypotenuse of one of them – the unknown side of an isosceles triangle, leg of a given height h. The second leg is unknown, label it H.

Consider the second triangle. Its hypotenuse is the basis of the total figures, one of the legs is equal to h. The other leg is the difference a – x. By the Pythagorean theorem, write down two equations relative to the unknown a and x:A2 = x2 + h2;c2 = (a - x)2 + h2.

Let the base equals 10 and height 8, then:A2 = x2 + 64;100 = (a - x)2 + 64.

Express artificially introduced variable x from the second equation and substitute it in the first and x = 6 → x = a – 6а2 = (a - 6)2 + 64 → a = 25/3.

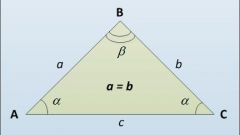
The base and one of the equal angles α.Draw a height to the ground, consider one of the right triangles. The cosine of the lateral angle is equal to the ratio of the adjacent leg to the hypotenuse. In this case, the leg equal to half the base of an isosceles triangle, and the hypotenuse is the side:(c/2)/a = cos α → a = c/(2•cos α).

The base and opposite angle β.Drop a perpendicular on the base. A corner of one of the resulting right triangles is equal to β/2. The sine of that angle is the ratio of the opposite leg to the hypotenuse a, where:a = c/(2•sin(β/2))