You will need
- Table Bradis, calculator.
Instruction
1
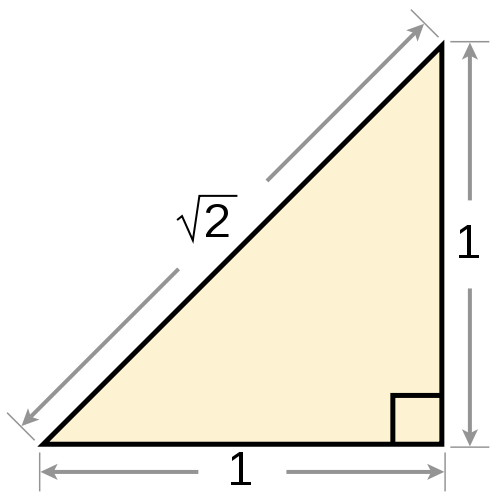
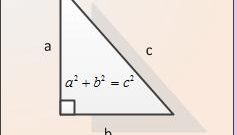
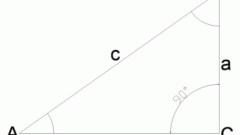
If you want to calculate the hypotenuse by the Pythagorean theorem, use the following algorithm:- Determine the triangle which sides are legs and which is the hypotenuse. The two sides forming the angle to ninety degrees and have each of the the remaining third side of the triangle is the hypotenuse. (see figure)- Lift the second degree, each leg of this triangle, that is, multiply their value by yourself. Example 1. Let we need to calculate the hypotenuse if one leg of the triangle is 12 cm and another 5 cm first, the squares of the legs is equal to: 12*12=144 cm and 5*5 = 25 cm Next, determine the sum of squares of other two sides. A certain number is the square of the hypotenuse, then you need to get rid of the degree numbers to find the length of this side of the triangle. To do this, remove from under the square root value of the sum of squares of other two sides. Example 1. 144+25=169. The square root of 169 is 13. Therefore, the length of the hypotenuse is equal to 13 cm.
2
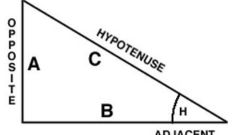
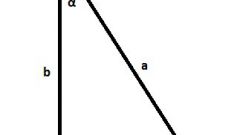
Another method of calculating the length of the hypotenuse is in terms of sine and cosine of angles in the triangle. By definition, the sine of the angle alpha is the ratio of the opposite leg to the hypotenuse. That is, looking at the figure, sin a = SV / AV. Hence, the hypotenuse AB = DM / sin a.Example 2. If the angle a is 30 degrees, and opposite him the side - 4 cm Need to find the hypotenuse. Solution: AB = 4 cm/ sin 30 = 4 cm / 0.5 = 8 cm Answer: the length of the hypotenuse is equal to 8 cm.
3
The same method of finding the hypotenuse from the definition of the cosine of the angle. The cosine of an angle is the ratio adjacent thereto of the leg and the hypotenuse. That is, cos a = AC/AB, hence AB = AC/cos. Example 3. In triangle ABC, AB is the hypotenuse, angle ABC is 60 degrees, side AC is 2 cm Find AB.
Solution: AB = AC/cos 60 = 2/0,5 = 4 cm answer: the hypotenuse is 4 cm in length.
Solution: AB = AC/cos 60 = 2/0,5 = 4 cm answer: the hypotenuse is 4 cm in length.
Useful advice
When finding the values of the sine or cosine of an angle use a table of sines and cosines, or table Bradis.