Instruction
1
To find the length of the base of the triangle at the sides without any additional parameters only if they are represented by their coordinates in a two - or three-dimensional system. For example, suppose the three-dimensional coordinates of the point A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) and C(X₃,Y₃,Z₃), the segments between them form the side. Then, you know, and the coordinates of the third side (the base) is formed by the segment AC. To calculate its length, find the difference between the coordinates of the points along each axis, the values obtained erect in the square, and fold, and the result extract the square root of a: AC = √((X₃-X₁)2 + (Y₃-Y₁)2 + (Z₃ Is Z₁)2).
2
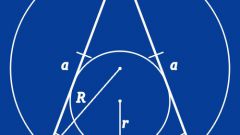
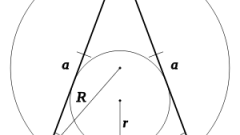
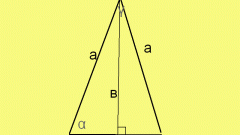
If you know only the length of each of the sides (a) to calculate the length of the base (b) need more information - for example, the magnitude of the angle between them (γ). In this case you can use the theorem of cosines, which implies that the length of a side of a triangle (not necessarily isosceles) is equal to the square root of the sum of the squares of the lengths of two other sides, from which is subtracted twice the product of their lengths into the cosine of the angle between them. Since in an equilateral triangle the length of a formula involved parties are the same, it can be simplified: b = a*√(2*(1-cos(γ))).
3
For the same initial data (the length of the sides equal to a, the angle between them is equal to γ) can be used and the theorem of sines. To do this, find twice the product of the known length of side to the sine of half the angle lying opposite the base of the triangle: b = 2*a*sin(γ/2).
4
If in addition the lengths of the sides (a) given the angle (α) adjacent to the base, we can apply the theorem on projections: the length of a side is equal to the sum of the other two sides into the cosine of the angle which they form with the party. Since in an equilateral triangle these sides, as the angles involved are of the same magnitude, then write the formula: b = 2*a*cos(α).