You will need
  • Paper, pen, table of sines (in the Internet)
Instruction
1
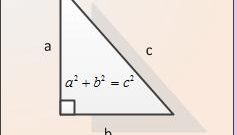
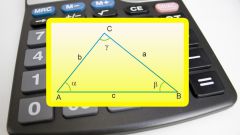
We denote the sides of a right triangle by the small letters a, b, and c and angles opposite them, respectively, And, And C. and Suppose known side and opposite him the angle A.
2
Then find the sine of the angle A. To do this, the table of sines we find the value for a given corner. For example, if the angle A is 28 degrees, its sine is 0.4695.
3
Knowing the other two sides and the sine of the angle A, find the hypotenuse, dividing side a by the sine of angle A. (c = a/sin A). The meaning of this action becomes intelligible if we remember that the sine of an angle And it's opposite leg to the hypotenuse (C). That is, sin A=a/C, and this equation is easily derived formula we just used.
4
If you know a leg and the adjacent angle, then before you begin any of the steps 2 and 3, find the angle A. To do this, from 90 (in a right triangle the sum of the acute angles is 90 degrees) subtract the value of a known angle. That is, if we know the angle has degree measure 62, the 90 - 62 = 28, that is, the angle A is 28 degrees. Calculating the angle And just repeat the steps in steps 2 and 3, and get the length of the hypotenuse C.