Instruction
1
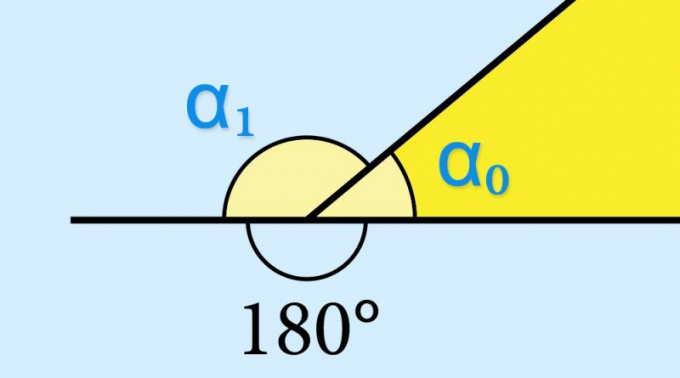
If you know the sine of an interior angle (α₀) geometric shapes to calculate something is not necessary - the sine of the corresponding external angle (α₁) will have exactly the same value: sin(α₁) = sin(α₀). This is determined by the properties of the trigonometric functions sin(α₀) = sin(180°-α₀). If you wanted to find out, for example, cosine or tangent of the outer edge, this value would need to be taken with the opposite sign.
2
There is a theorem that in a triangle the sum of any two interior angles equal the exterior angle of a third vertex. Use it in that case, if the magnitude of the internal angle corresponding to the considered external (α₁), unknown, and the angles (β₀ and γ₀) the other two vertices are given in the conditions. Find the sine of the sum of the known angles: sin(α₁) = sin(β₀+γ₀).
3
The task with the same initial conditions as in the previous step, has another solution. It follows from another theorem - the sum of the interior angles of a triangle. As this amount is, according to the theorem, must be equal to 180°, the value of the unknown internal angle can be represented using two known (β₀ and γ₀) - it will be equal to 180°-β₀-γ₀. This means that you can use the formula from the first step, replacing in this the value of internal angle of this expression: sin(α₁) = sin(180°-β₀-γ₀).
4
In a regular polygon the value of the external angle at any vertex is equal to the size of the Central angle and, therefore, can be calculated using the same formula that he did. Therefore, if the conditions of the problem given the number of sides (n) of the polygon, when computing the sine of any angle (α₁) assume that its value is equal to the turnover divided by the number of sides. Full rotation in radians is expressed by twice the number PI, so the formula should look like this: sin(α₁) = sin(2*π/n). When calculating in degrees double PI replace 360°: sin(α₁) = sin(360°/n).