Instruction
1
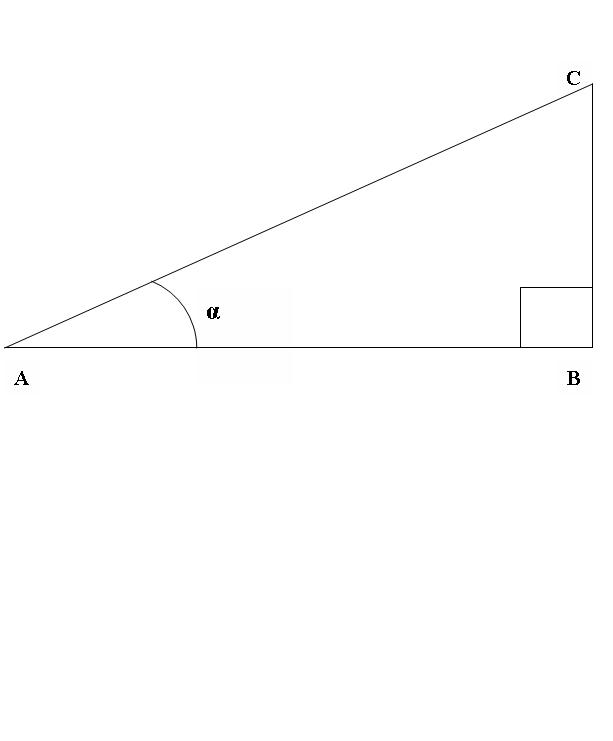
Draw a right triangle ABC, where angle ABC is a straight line (Fig.1). Consider the ratio of the sineand cosineand angle CAB. According to the above definition
sin CAB=BC/AC cos CAB=AB/AC.
sin CAB=BC/AC cos CAB=AB/AC.
2
Remember the Pythagorean theorem - AB^2 + BC^2 = AC^2, where ^2 is the operation of squaring.
Divide left and right side of the equation by the square of the hypotenuse AC. Then the previous equation will look like this:
AB^2/AC^2 + BC^2 AC^2 = 1.
Divide left and right side of the equation by the square of the hypotenuse AC. Then the previous equation will look like this:
AB^2/AC^2 + BC^2 AC^2 = 1.
3
For convenience, we rewrite the equation obtained in step 2, as follows:
(AB/AC)^2 + (BC/AC)^2 = 1.
According to the definitions given in step 1, we get:
cos^2(CAB) + sin^2(CAB) = 1, i.e.
cos(CAB)=SQRT(1-sin^2(CAB)), where SQRT is the operation of taking the square root.
(AB/AC)^2 + (BC/AC)^2 = 1.
According to the definitions given in step 1, we get:
cos^2(CAB) + sin^2(CAB) = 1, i.e.
cos(CAB)=SQRT(1-sin^2(CAB)), where SQRT is the operation of taking the square root.
Useful advice
The magnitude of the sine and cosine of any angle cannot be greater than 1.