Instruction
1
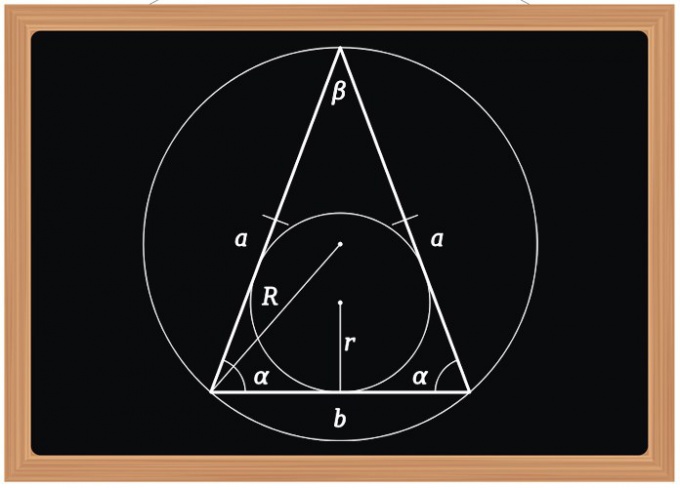
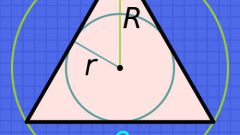
The length of the side (A) of an equilateral triangle to find the radius of the inscribed circle (r). To do so, increase it to six times and divide by the square root of triples: A = r*6/√3.
2
Knowing the radius of the circumscribed circle (R), too it is possible to calculate the length of side (A) right triangle. This radius is twice that used in the previous formula, so triple it and also divide by the square root of triples: A = R*3/√3.
3
The perimeter (P) of an equilateral triangle to calculate the length of its side (A) is even simpler, because the lengths of the sides in this figure are the same. Just divide the perimeter into three pieces: A = R/3.
4
In an isosceles triangle the calculation of the length of the sides of known perimeter is a bit more complicated - you need to know more and a length of at least one of the parties. If you know the length of side A lying in the base of the figure, the length of any side (In) find halving the difference between the perimeter (P) and the size of the base: B = (R-A)/2. And if you know the side, the length of the base define by subtracting from the perimeter to twice the length of the side: A = R-2*V.
5
Knowledge area (S) occupied on the plane right triangle, is also sufficient for finding the lengths of its sides (A). Extract the square root of the area ratio and the square root of three, and the result double A = 2*√(S/√3).
6
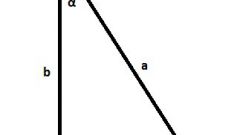
In a right triangle, unlike any other, to calculate the length of one of the parties is sufficient to know the lengths of the other two. If the target side is the hypotenuse (C), to do this, find the square root of the sum of the lengths of the known sides (A and b) squared: C = √(A2+B2). But if you want to calculate the length of one of the other two sides, then the square root must be obtained from the difference of the squares of the lengths of the hypotenuse and another side: A = √(C2-B2).