Instruction
1
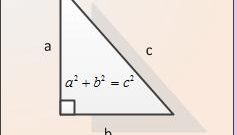
Let's consider a given triangle with vertices A, B and C, and the angle ABC is a straight line, that is equal to ninety degrees. The sides AB and BC of the triangle are called the legs, and the side AC is the hypotenuse. For starters, look at the conditions of the problem and determine the magnitude of any side of triangle you are aware of, and which way you want to find. For a successful solution you need to know the lengths of two of the three sides of the triangle. You must know either the lengths of two sides, or the length of one of the legs and the length of the hypotenuse.
2
The length of the sides of a right triangle is calculated by the theorem of the Greek mathematician Pythagoras. This theorem specifies the relationship between the legs and the hypotenuse: the hypotenuse squared is equal to the sum of the squares of the legs. If you want to find the leg length (for example, side AB), the formula for it will look like this: AB = √(AC2 - BC2). To calculate it on the calculator, but in some cases can be in the mind. For example, for a triangle with sides BC = 4 and AC = 5 leg length AB is also an integer and therefore can be easily calculated by the above formula. AB = √(25 - 16) = 3.
3
If you want to find the length of the hypotenuse, then this can be done according to the following formula derived from the Pythagorean theorem: AC = √(AB2 + BC2). So, for a triangle with sides AB = 5 and BC = 12, the result obtained AC = √(25 + 144) = 13. Depending on the conditions of the problem use the result in further calculations, or write as your answer.
Note
Mathematics is often inappropriate calculation of the exact values of square roots and cube roots. If the resulting formula result is not an integer or a fractional number, it is better to leave the square root symbol and not think of the answer on the calculator. For example, record the response as AC = √7 instead of having to calculate its value — 2,6457.