Instruction
1
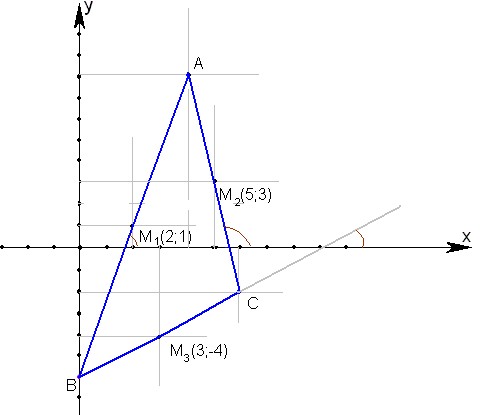
You are given the coordinates of three points. Denote them as (x1, y1), (x2, y2), (x3, y3). It is assumed that these points are the vertices of some triangle. The task is to write the equations of its sides, or rather the equations of those straight, where are these parties. These equations should be:
y = k1*x + b1;
y = k2*x + b2;
y = k3*x + b3.Thus, you have to find the angular coefficients k1, k2, k3 and offset b1, b2, b3.
2
Make sure that all points are distinct. If any two match, then the triangle degenerates into a line segment.
3
Find the equation of the line passing through the points (x1, y1), (x2, y2). If x1 = x2, then the required straight vertical and its equation is x = x1. If y1 = y2, the direct horizontal and its equation is y = y1. In the General case, these coordinates will not be equal to each other.
4
Substituting the coordinates (x1, y1), (x2, y2) in the General equation of a straight line, you will get a system of two linear equations:k1*x1 + b1 = y1;
k1*x2 + b1 = y2.Subtract one equation from the other and solve the resulting equation for k1:k1*(x2 - x1) = y2 - y1 therefore, k1 = (y2 - y1)/(x2 - x1).
5
Substituting the expression in any of the original equations, find an expression for b1:((y2 - y1)/(x2 - x1))*x1 + b1 = y1;
b1 = y1 - ((y2 - y1)/(x2 - x1))*x1.Since we already know that x2 ≠ x1, we can simplify the expression by multiplying y1 (x2 - x1)/(x2 - x1). Then for b1 you will get the following expression:b1 = (x1*y2 - x2*y1)/(x2 - x1).
6
Check is the third of the given points to the found line. To do this, substitute the values of (x3, y3) in the derived equation and see whether they are equal. If it is observed, therefore all three points are collinear, and the triangle degenerates into a line segment.
7
In the same way as described above, output equation for a straight line passing through the points (x2, y2), (x3, y3) and (x1, y1), (x3, y3).
8
The final form of the equations for the sides of a triangle given coordinates of vertices, as follows:(1) y = ((y2 - y1)*x + (x1*y2 - x2*y1))/(x2 - x1);
(2) y = ((y3 - y2)*x + (x2*y3 - x3*y2))/(x3 - x2);
(3) y = ((y3 - y1)*x + (x1*y3 - x3*y1))/(x3 - x1).