How to find the formula area of isosceles triangle

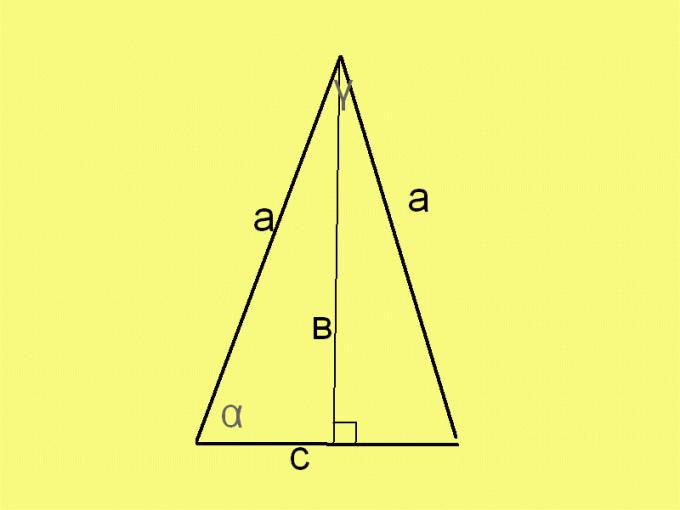
Under the height of an isosceles triangle usually mean the length of the perpendicular on the "unequal" side, and under the base is the length of this side. For finding the area of an isosceles triangle, label the length of its equal sides by a, the length of the base – through with, and the length of the altitude through C. In this case, the formula to calculate square (N) will look as follows:P = ½ * C *

To find the formula for area of an isosceles triangle using the base and the length of the equal sides, use the Pythagorean theorem and the fact that the ground divided by the height in half. We get the following expression for the height:h = √(A2 - C2/4), substituting it into the above formula, we get:P = ½ * C * V(A2 - C2/4).

For finding area of isosceles triangle based on Heron formula, substitute into it the lengths of the sides of an isosceles triangle given the fact that two of them are equal. After a number of reductions will be:P = ½ * C * √[(a - C)*(a + C)].It is easy to see that both formulas are identical since the difference of the squares of the first formula is simply decomposed into the product of the sum and difference.

To find the formula for area of an isosceles triangle using the values of catch, label:
α - the angle between the equal sides and the base;
γ - the angle between the equal sides.Then, using basic trigonometric ratios, we get:P = ½ * a * s * cos(γ/2),P = ½ * C * a * sin(α/2),P = ½ * S2 / tg(γ/2),P = ½ * S2 * tg(α/2),N = A2 * sin(γ/2) * cos(γ/2),N = A2 * sin(α/2) * cos(α/2),

The above formulas cover all the main options calculate area isosceles triangle. However, if we consider that the height of the isosceles triangle is at the same time its bisector and median, you can "take" a couple of formulas, replacing
P = ½ * C *
marking height on marking medians or bisectors.