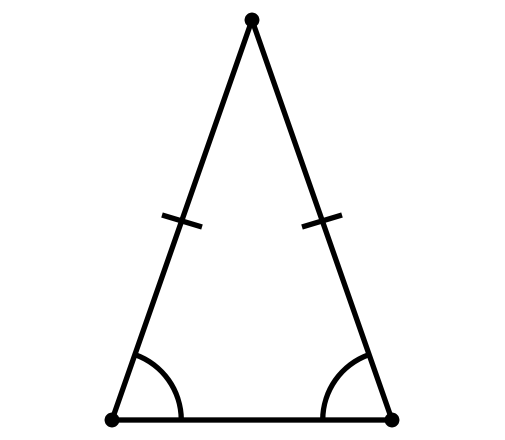
Instruction
1
Method 1. Classic.
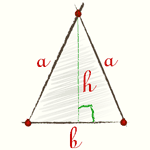
Area of isosceles triangle can be calculated by the classic formula: polypropelene the base of the triangle to its height.
S=1/2bh
b is the length of the base of the triangle;
h - the length of the height of treugolnika.
Area of isosceles triangle can be calculated by the classic formula: polypropelene the base of the triangle to its height.
S=1/2bh
b is the length of the base of the triangle;
h - the length of the height of treugolnika.
2
Method 2. Heron's Formula.
a - length one of the equal sides of the triangle;
b - length of base of triangle.
a - length one of the equal sides of the triangle;
b - length of base of triangle.
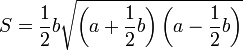
3
Method 3. It follows from the formula of method 1.
α is the angle between the side and the base;
γ - the angle between the equal sides.
α is the angle between the side and the base;
γ - the angle between the equal sides.
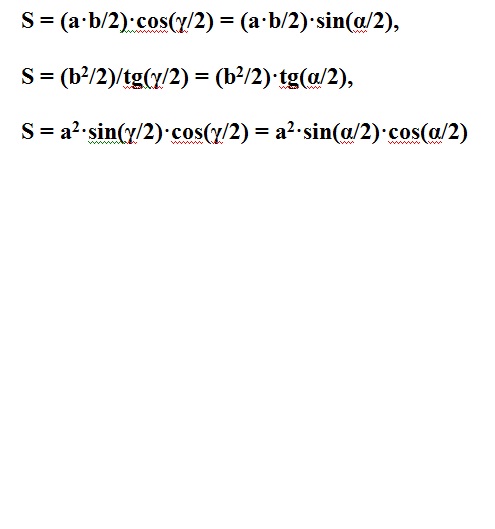
Note
There are signs of an isosceles triangle:
1) an isosceles triangle has 2 equal angles;
2) the height of the triangle coincides with its median;
3) the Height of a triangle coincides with its bisector;
4) angle Bisector of a triangle coincides with its median;
5) the isosceles triangle the median is equal to 2;
6) isosceles triangle 2 equal height;
7) an isosceles triangle 2 equal bisectors.
1) an isosceles triangle has 2 equal angles;
2) the height of the triangle coincides with its median;
3) the Height of a triangle coincides with its bisector;
4) angle Bisector of a triangle coincides with its median;
5) the isosceles triangle the median is equal to 2;
6) isosceles triangle 2 equal height;
7) an isosceles triangle 2 equal bisectors.