Instruction
1
Draw isosceles trapezoid. Given the area of a trapezoid is S, the height of the trapezoid is h and lateral side is a. Lower the height of the trapezoid to a larger base. The larger base will be divided into the segments m and n.

2
To determine the length of both bases (x, y), apply the property of isosceles trapezoids the formula for calculating the area of a trapezoid.
3
According to the property of isosceles trapezoids the segment of n equal to half-difference of the bases x and y. Consequently, the smaller base of trapezoid y can be represented in the form of a difference larger base and the segment n, multiplied by two: y = x - 2*n.
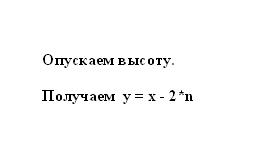
4
Find the unknown lower segment n. To do this, calculate one side of the resulting right triangle. The triangle formed by the height h (side), side a (hypotenuse) and cut – n side). According to the Pythagorean theorem, the unknown side n2 = a2 - h2. Substitute known numeric values, and calculate the square of side n. Take the square root of the resulting value – this is the length of the segment n.
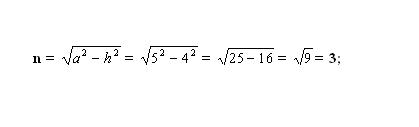
5
Substitute the value obtained in the first equation to calculate y. Area of a trapezoid is calculated by the formula S = ((x + y)*h)/2. We Express the unknown variable: y = 2*S/h.
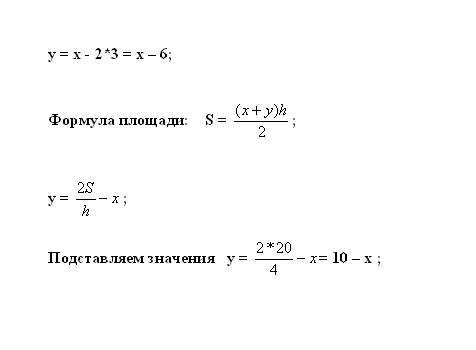
6
Write both equations in the resulting system. Substituting the known values, find two unknown values in two equations. The obtained solution of the system x represents the length of the long base, and y is the smaller base.