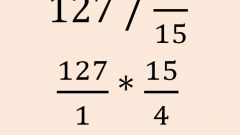You will need
- - a piece of paper;
- - a pen or pencil.
Instruction
1
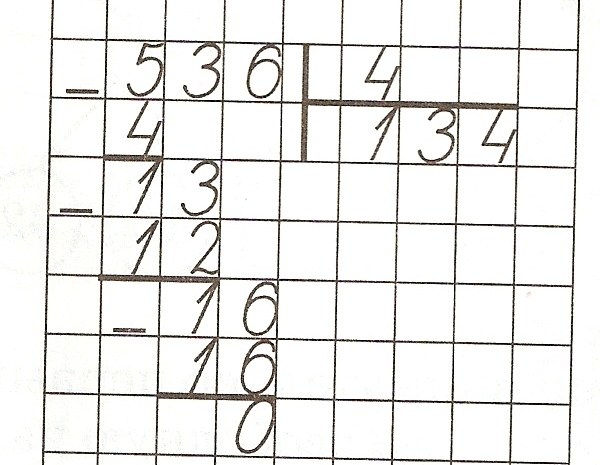
Division by a single-digit number without remainder - the simple case for divide area. For example, divide 536 by 4. To do this, write them side by side on one line, and not to mix, put between them the area. Under the horizontal line will write the quotient or result of division.
First, divide the first digit of the dividend, that is, 5 to 4. Write below the line 1, under five - four and subtract from the first second. The difference record at the bottom. Next to it write the next figure of the dividend, which is 3. It turns out 13. Divide by 4, the result - three - write the right and balance again carry down. Transfer to it the last digit of the original number, you get 16. Divide by 4 and record the four last digit of the answer. It turned out that one-fourth of the 536 is 134.
To check the result, multiply the column 134 and 4. Work 536. If the check failed, look for error in the transference of numbers when dividing by the area.
First, divide the first digit of the dividend, that is, 5 to 4. Write below the line 1, under five - four and subtract from the first second. The difference record at the bottom. Next to it write the next figure of the dividend, which is 3. It turns out 13. Divide by 4, the result - three - write the right and balance again carry down. Transfer to it the last digit of the original number, you get 16. Divide by 4 and record the four last digit of the answer. It turned out that one-fourth of the 536 is 134.
To check the result, multiply the column 134 and 4. Work 536. If the check failed, look for error in the transference of numbers when dividing by the area.
2
Division round numbers is fundamentally no different. Just before the beginning of the division get rid of the extra zeros. By such means the digits that are in both numbers. For example, if it is necessary to divide 371000 700, before dividing by the area cross out the last two zeros in each number. That is, divide by 7 3710. It is necessary to cross out exactly the same number of zeros, otherwise the result is incorrect.
3
When dividing proper fractions do the reverse operation: add orders in the dividend to correspond to the divider. For example, if you divide 5 by 16, then add one zero. If 5 should be divided into 160, then add two zeros. But don't forget to put a full stop and the same number of zeros in the private. In the first case, the response will start with tenths, the second hundredths with. In other words, the division area is the simplest way to correct the fraction to a decimal.