Instruction
1
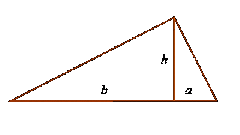
To find the sides of the rectangle need to consider one of those right triangles. In it, the hypotenuse is the diagonal ofth rectangle, and the sides of his parties. Before the calculation of numeric values we need to find equations in General form. For each hand will be your equation. So, to get formulas in a right triangle, label each of the Latin letters a and b and the hypotenuse is C.
2
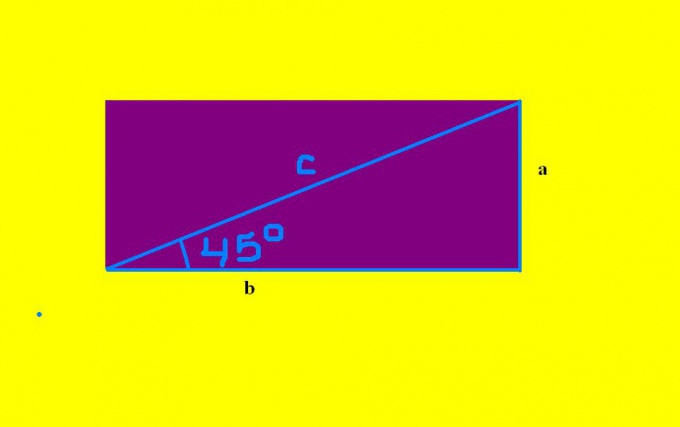
The solution of the problem consists of determining the sine and the Pythagorean theorem. Select any of the acute angles in the triangle (they are equal), with whom you will work. Define adjacent to it side and, opposite from it, the other leg. For example, suppose that adjacent to the angle, is side b, and opposite - side.
3
Further, based on the definition of the sine, which States that the sine of an angle in a right triangle is equal to the ratio of the opposite leg to the hypotenuse, write down the equation: sin 45 = a/C. In this example, the condition is known: the sine of the angle (sin 45 ~0,7) and hypotenuse s. Hence, we get the equation 0,7=a/C from where a=0,7 p. it Remains to substitute the numerical value of p. was Found side a will be equal to the parallel side of the rectangle. Thus, the two known hand shapes.