Instruction
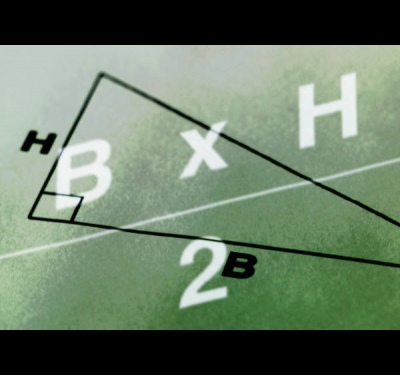
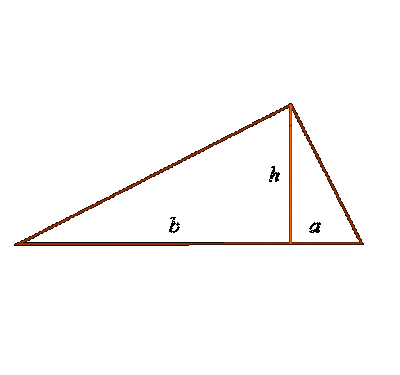
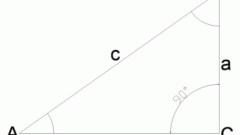
The angles opposite sides a and b denote respectively through A and B. the Hypotenuse is, by definition, is the side of a right triangle that is opposite the right angle (with the other sides of the triangle the hypotenuse forms a sharp corner). The length of the hypotenuse is denoted by S.

You will need:
Calculator.
Calculator.

Check which of the following cases corresponds to the condition of your problem and depending on this, refer to the relevant paragraph. Find out which values in the triangle you are aware of.
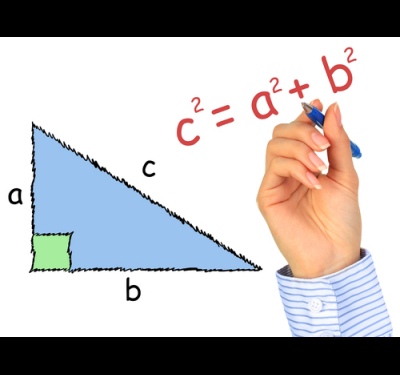
Use to calculate the sides of the following expression: a=sqrt(c^2-b^2), in that case, if you are aware of the magnitude of the hypotenuse and other leg. This expression is obtained from the Pythagorean theorem, which States that the square of the hypotenuse of a triangle is equal to the sum of the squares of the legs. The operator sqrt means square root. The sign "^2" means squaring.

Use the formula a=c*sinA if you know the hypotenuse (c) and the angle opposite to the desired side (this angle we have designated as A).
The expression a=c*cosB use for finding what to do if you know the hypotenuse (c) and the angle adjacent the desired side (this angle we have designated as B).
Calculate the leg by the formula a=b*tgA in the case when, given a side and angle b opposite to the desired side (this corner we have agreed to designate A).
The expression a=c*cosB use for finding what to do if you know the hypotenuse (c) and the angle adjacent the desired side (this angle we have designated as B).
Calculate the leg by the formula a=b*tgA in the case when, given a side and angle b opposite to the desired side (this corner we have agreed to designate A).

Please note:
If your problem side is not one of the described methods, most likely, it can be reduced to any of them.
If your problem side is not one of the described methods, most likely, it can be reduced to any of them.
Useful tips:
All these expressions are obtained from the well-known definitions of trigonometric functions, so even if you forget some of them, you can by simple operations, it quickly withdraw. Also, it is useful to know values of trigonometric functions for the most common angles 30, 45, 60, 90, 180 degrees.
All these expressions are obtained from the well-known definitions of trigonometric functions, so even if you forget some of them, you can by simple operations, it quickly withdraw. Also, it is useful to know values of trigonometric functions for the most common angles 30, 45, 60, 90, 180 degrees.