How to find the third side if we know the angle

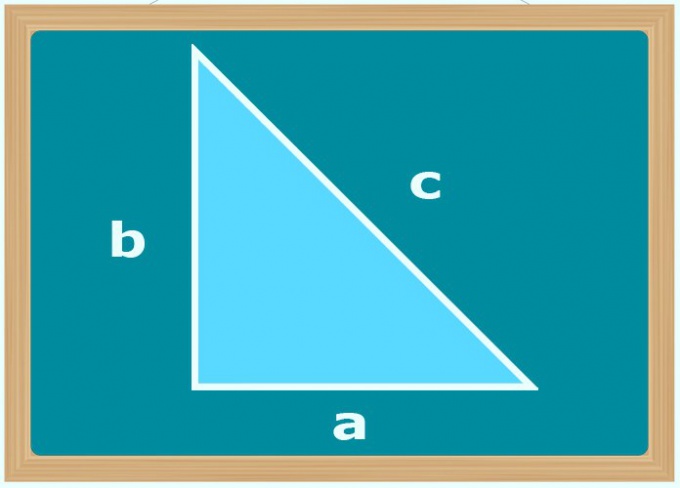
If the only known angle is 90°, and in the conditions given the lengths of two sides of trianglea square (b and c), determine which of them is the hypotenuse - it must be the side of the big sizes. Then use the Pythagorean theorem and calculate the length of the unknown side (a) square root of difference of squares of the lengths of larger and smaller parties: a = √(c2-b2). However, you can not figure out which side is the hypotenuse, and extract the root of the module of the difference of the squares of their lengths.

Knowing the length of the hypotenuse (c) and the angle (α) lying next to your sideand (a) use in the calculation of the trigonometric definition of the sine function through the sharp corners of rectangular tregon. This definition says that the sine of the known angle conditions are equal to the ratio between the lengths of the opposite legand the hypotenuse, and therefore, to calculate the desired values multiply the sine to the length of the hypotenuse: a = sin(α)*C.

If in addition the length of the hypotenuse (C) is given the value of the angle (β), adjacent to the desired leg (a) use the definition of another function - cosine. It sounds exactly the same, and therefore, before the calculation, simply replace the function notation and angle in the formula from the previous step: a = cos(β)*C.

The cotangent function will help calculate the length of sidea (a), if the conditions the previous step replaced by a second hypotenuse legom (b). By definition, the value of this trigonometric function equal to the ratio of the lengths of the legs, so multiply the cotangent of an angle is known on the length of the known sides: a = ctg(β)*b.

Use the tangent to calculate the length of sidea (a), if the conditions is the value of angle (α) lying in the opposite apex of the triangleof the polygon, and the length of the second legand (b). According to the definition of the tangent is known of the conditions of an angle is the ratio of the length of the required side to the length of the known legand, therefore, multiply the value of this trigonometric function from a given angle to the length of the known sides: a = tg(α)*b.