Instruction
1
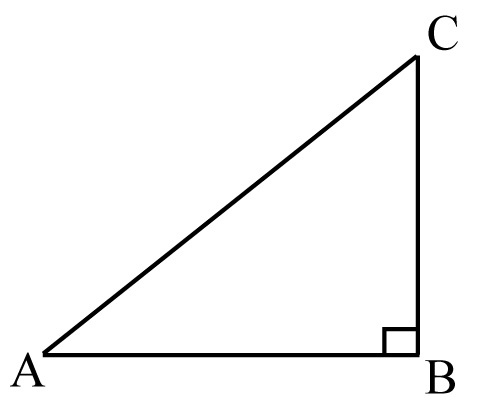
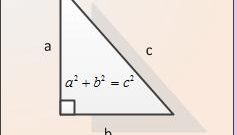
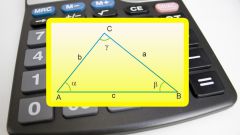
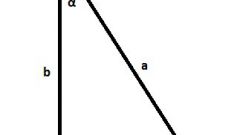
The lengths of the legs and the hypotenuse are related by, which is described by the Pythagorean theorem. Algebraic formulation: "In a right triangle the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides."
The formula of Pythagoras looks like this:
c2 = a2 + b2,
where C is the length of the hypotenuse, a and b are the lengths of the legs.
The formula of Pythagoras looks like this:
c2 = a2 + b2,
where C is the length of the hypotenuse, a and b are the lengths of the legs.
2
Knowing the length of sides by using the Pythagorean theorem to find the hypotenuse of a right triangle:
c = √(a2 + b2).
c = √(a2 + b2).
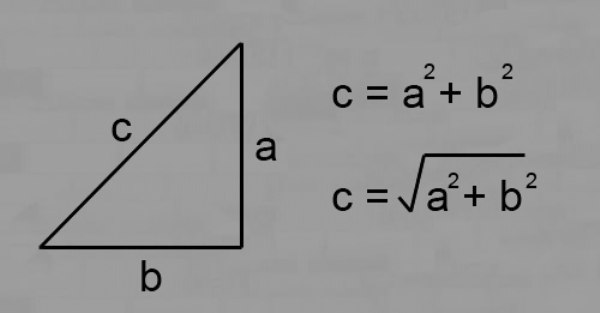
3
Example. The length of one of the legs is equal to 3 cm, the length of the other 4 cm (the Sum of their squares is equal to 25 cm2:
9 cm2 + 16 cm2 = 25 cm2.
The length of the hypotenuse in this case is the square root of 25 cm 2 - 5 cm therefore, the length of the hypotenuse equal to 5 cm.
9 cm2 + 16 cm2 = 25 cm2.
The length of the hypotenuse in this case is the square root of 25 cm 2 - 5 cm therefore, the length of the hypotenuse equal to 5 cm.