Instruction
1
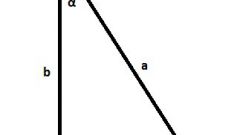
The sides of a right triangle adjacent to the right angle (AB and BC are called the legs. Side lying opposite the right angle is called the hypotenuse (AC).
Let we know the hypotenuse AC of the right triangle ABC: AC| = c. We denote the angle with vertex at point A as a ∟α, the angle with vertex at point B as ∟β. We need to find the lengths |AB| and |BC| of the other two sides.
Let we know the hypotenuse AC of the right triangle ABC: AC| = c. We denote the angle with vertex at point A as a ∟α, the angle with vertex at point B as ∟β. We need to find the lengths |AB| and |BC| of the other two sides.
2
Let known one of the legs of a right triangle. Assume |BC| = b. Then we can use the Pythagorean theorem that the hypotenuse squared is equal to the sum of the squares of the legs: a^2 + b^2 = c^2. From this equation we find unknown side |AB| = a = √ (c^2 - b^2).
3
Let you know one of the angles of a right triangle, suppose ∟α. Then the other two sides AB and BC of the triangle ABC can be found using trigonometric functions. So we get: sine ∟α equal to the ratio of the opposite leg to the hypotenuse sin α = b / c cosine ∟α equal to the ratio of adjacent sides to the hypotenuse cos α = a / c. Hence, we find the required lengths of the sides: |AB| = a = C * cos α, |BC| = b = c * sin α.
4
Let you know the ratio of sides k = a / b. Solve problems using trigonometric functions. The ratio a / b is none other than the cotangent ∟α: the ratio of the adjacent leg to the opposite ctg α = a / b. In this case, from this equality we Express a = b * ctg α. And substitute in the Pythagorean theorem a^2 + b^2 = c^2:
b^2 * ctg^2 α + b^2 = c^2. Make b^2 outside the brackets, we get b^2 * (ctg^2 α + 1) = c^2. And easily get the length of leg b = c / √(ctg^2 α + 1) = c / √(k^2 + 1), where k is a predetermined ratio of the legs.
By analogy, if you know the ratio of each b / a, we solve the problem with the use of trigonometric functions the tangent tg α = b / a. Substitute the value b = a * tg α in the Pythagorean theorem a^2 * tg^2 α + a^2 = c^2. Hence a = c / √(tg^2 α + 1) = c / √(k^2 + 1), where k is a predetermined ratio of the legs.
b^2 * ctg^2 α + b^2 = c^2. Make b^2 outside the brackets, we get b^2 * (ctg^2 α + 1) = c^2. And easily get the length of leg b = c / √(ctg^2 α + 1) = c / √(k^2 + 1), where k is a predetermined ratio of the legs.
By analogy, if you know the ratio of each b / a, we solve the problem with the use of trigonometric functions the tangent tg α = b / a. Substitute the value b = a * tg α in the Pythagorean theorem a^2 * tg^2 α + a^2 = c^2. Hence a = c / √(tg^2 α + 1) = c / √(k^2 + 1), where k is a predetermined ratio of the legs.
5
Consider special cases.
∟α = 30°. Then |AB| = a = c * cos α = c * √3 / 2; |BC| = b = c * sin α = c / 2.
∟α = 45°. Then |AB| = |BC| = a = b = c * √2 / 2.
∟α = 30°. Then |AB| = a = c * cos α = c * √3 / 2; |BC| = b = c * sin α = c / 2.
∟α = 45°. Then |AB| = |BC| = a = b = c * √2 / 2.
Note
Square roots are extracted with a positive sign, because length cannot be negative. It seems obvious, but this error is very common, if to solve the problem automatically.
Useful advice
For finding the legs of a right triangle is convenient to use formula bring: sin β = sin (90° - α) = cos α; cos β = cos (90° - α) = sin α.