How to find the length of the leg

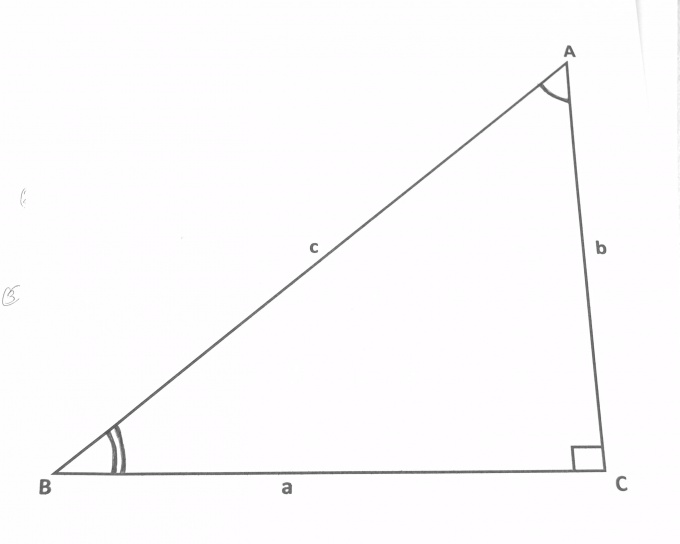
Let the sides of the triangle are labeled a and b, hypotenuse, and opposite sides of the angles A, B and C. If we know the hypotenuse (C) and second leg (b), you should use the Pythagorean theorem: the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides (c2 = a2 + b2). It follows that to calculate the side a, you must remove the root from the difference of the square of the hypotenuse and square of the second leg (a = v(c2-b2)).

If you know the hypotenuse (C) and the angle lying opposite the side (A), the length of which you want to find, you can use the formula a = PA. In order to determine the sine of the angle, look in a table of sines and just look at the value corresponding to the degree measure of the angle. If, say, angle A is 43 degrees, its sine is equal to 0.682. Taken from the table the value of the sine and multiply by the length of the hypotenuse and get the length of the leg.

If you know the hypotenuse (C) and the angle adjacent to the desired side, (B) then the easiest way will be to repeat step 2, pre-calculate the opposite angle. From 90 (the sum of the acute angles in the triangle is 90 degrees), subtract the degree measure of the adjacent angle.

If you know the second leg (b) and the angle opposite the side length of which should find,(A) it is necessary to use the formula: a = b tgA. That is, the first table of tangents to find the tangent ratio for a known angle, and then multiply this value by the length of the second leg.