You will need
- - Knowledge of two of the three sides of a right triangle;
- - Knowledge of the angles of a triangle.
Instruction
1
Method 1. The use of the Pythagorean theorem. The theorem States that the hypotenuse squared is equal to the sum of the squares of the legs. It follows that any of the sides of a right triangle can be calculated, knowing the two other sides (Fig.2)
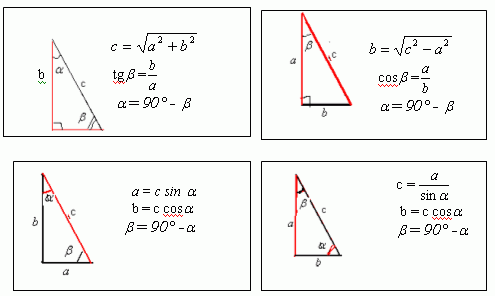
2
Method 2. Follows from the fact that the median drawn from the right angle to the hypotenuse forms between the 3 similar triangles (Fig. 3). In this figure, are similar triangles ABC, BCD and ACD.
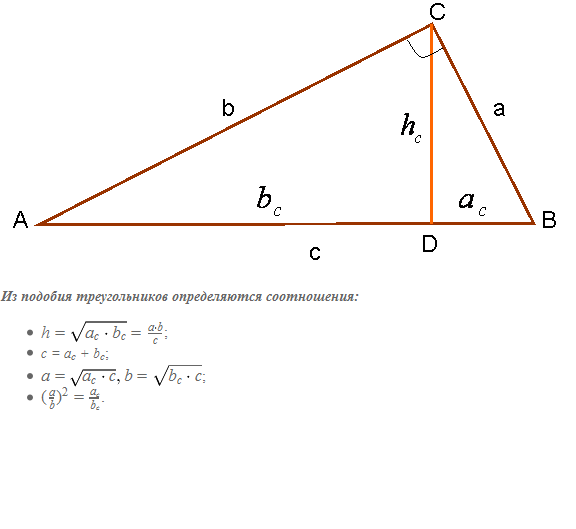
Note
When calculating sides of a right triangle can play knowing the signs:
1) If the leg of a right angle is opposite the angle of 30 degrees, it is equal to half the hypotenuse;
2) the Hypotenuse is always longer than any of the other two sides;
3) If you are around the right triangle described a circle, its centre must lie in the middle of the hypotenuse.
1) If the leg of a right angle is opposite the angle of 30 degrees, it is equal to half the hypotenuse;
2) the Hypotenuse is always longer than any of the other two sides;
3) If you are around the right triangle described a circle, its centre must lie in the middle of the hypotenuse.