How to find the projection of the leg on the hypotenuse

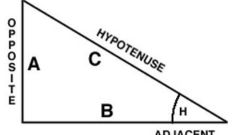
If the initial conditions of the problem given the length of the hypotenuse (C) and the leg (A), the projection of which (AC) is required to calculate, use one of the properties of a triangle. Take advantage of the fact that the geometric mean of the lengths of the hypotenuse and the desired projection is equal to the length of side: A = √(S*As). As the concept of "geometric mean" is equivalent to "the root of the product", for finding the projection of a side erect a square the length of the leg and divide the resulting value by the length of the hypotenuse: AC = (A/√a)2 = A2/S.

If the length of the hypotenuse is unknown, and given only the lengths of both legs (A and b), in calculating the length of the desired projection (AU) you can use the Pythagorean theorem. Express according to it the length of the hypotenuse using the length of the sides √(A2+B2) and substitute the resulting expression into the formula from the previous step: AC = A2/√(A2+B2).

If you know the length of the projection of one of the other two sides (Sun) and the length of the hypotenuse (C), the method of finding the length of the projection of the other side (As) obvious - just subtract from the second known value of the first: AC = -BC.

If the lengths of the legs is unknown, but their ratio (x/y) and the length of the hypotenuse (C), then use a couple of formulas from the first and third steps. According to the expression of a first step, the ratio of the projections of the other two sides (AC and BC) will be equal to the ratio of squares of their lengths: AC/BC = x2/y2. On the other hand, according to the formula from the previous step, As+Vs = S. In the first equality Express the length of an unnecessary projection through the desired and substitute the obtained value into the second equation: AU + AU*x2/y2 = AC*(1 + x2/y2) = P. From this equation, output the formula for finding the projection of the leg: AC = C/(1 + x2/y2).

If you know the length of the projection on the hypotenuse of one side (BC), and the length of the hypotenuse is not given in terms, but given the height (H) drawn from the right angle of the triangle, this will also be enough to calculate the length of the projection of the other side (As). Lift height in square and divide by the length of the projection is known: AC = D2/Sun.