How to find the tangent of the outer corner

If you continue any side of the polygon, at the point of junction with it of the adjacent sides get a straight angle, adjacent side divided into two - external and internal. The appearance is one of them, which lies outside the perimeter of geometric shapes. Its value is connected with internal dimensions a certain ratio, and the magnitude of the internal, in turn, associated with other parameters of the polygon. This relationship allows, in particular, to calculate the parameters of the polygon is the tangent of the outer corner.

How to find the tangent of the outer corner
How to find the tangent if we know the cosine
How to find the sine of the outer corner
How to calculate angle in triangle

Instruction

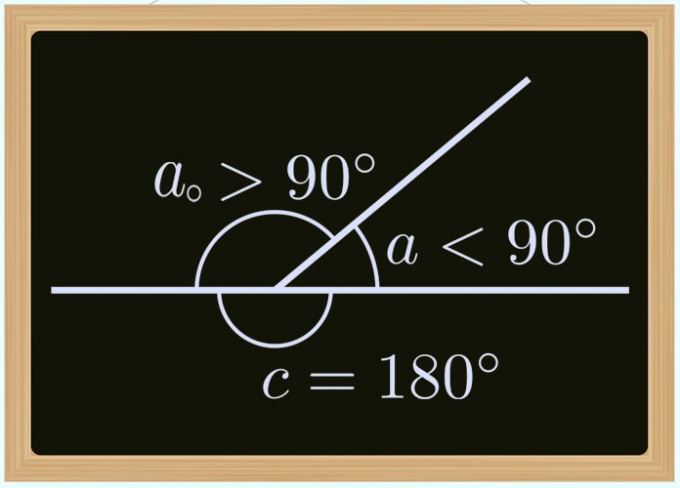
If you are aware of the magnitude of the corresponding outer corner (α₀) inner (α), come from the fact that together they always form a straight angle. The amount deployed to 180° in degrees, that corresponds to PI radians. This implies that the tangent of the external angle equal to the tangent of the difference between 180° and the included angle: tg(α₀) = tg(180°-α₀). In radians this formula should be written as: tg(α₀) = tg(π-α₀).

If the conditions of the problem given the magnitude of the tangent of the internal angle (α), tangent external (α₀) equal to her, but with changed sign: tg(α₀) = -tg(α).

Knowing the value of another trigonometric function expressing the internal angle (α), it is simplest to calculate the tangent of the external (α₀) use the inverse function to calculate the degree measure of the internal. For example, if you know the value of cosine, the angle can be found using the inverse cosine: α = arccos(cos(α)). Substitute the obtained value into the formula from the previous step: tg(α₀) = -tg(arccos(cos(α))).

In the triangle the value of any external angle (α₀) is equal to the sum of the two interior angles (β and γ), which lies in the other peaks. If these two values are known, compute the tangent of their sum: tg(α₀) = tg(β+γ).

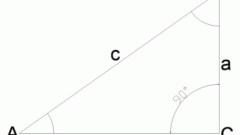
In a right triangle the value of the tangent of the outer corner (α₀) can be calculated from the lengths of the two shorter sides. Divide the length of one, which lies opposite the top outer corner (a) length adjacent to that vertex (b). The result should be taken with the opposite sign: tg(α₀) = -a/b.

If you want to calculate the tangent of the outer corner (α₀) of a regular polygon, is enough knowledge in the number of vertices (n) of this figure. By definition, any regular polygon can be inscribed in a circle, and any exterior angle is equal to the Central angle of the circle corresponding to the length of the sides. Because all parties are the same, the Central angle can be calculated by dividing a full revolution is 360° - the number of sides is 360°/n. Means for receiving a search value find the tangent of the ratio between 360° and the number of vertices: tg(α₀) = tg(360°/n).

Is the advice useful?