You will need
  • Textbook on trigonometry.
Instruction
1
In order to Express the tangent of an angle using a sine, you need to recall a geometric definition of tangent. So, the tangent of an acute angle in a right triangle is the ratio opposite over adjacent.
2
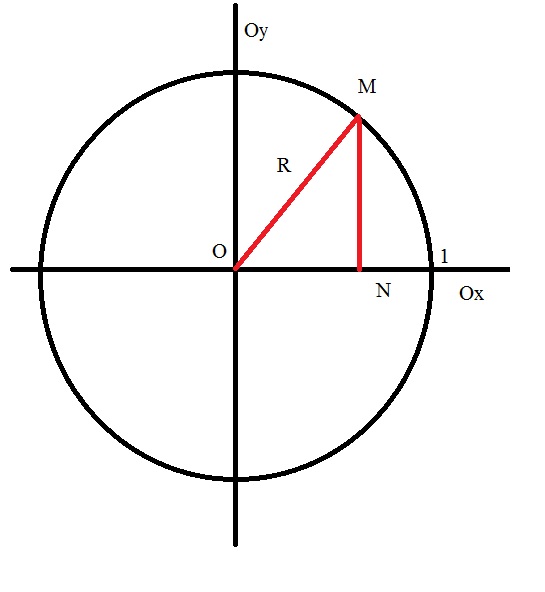
On the other hand, consider a Cartesian coordinate system where the unit circle is drawn with radius R=1 and with center in the origin. Take counterclockwise rotation as positive and the opposite direction negative.
3
Mark a certain point M on the circle. It will drop a perpendicular on the axis Oh, call it point N. get the triangle OMN, in which the angle ONM is a direct.
4
Now consider acute angle MON, by definition of sine and cosineand an acute angle in a right triangle
sin(MON) = MN/OM cos(MON) = ON/OM. Then MN= sin(MON)*OM and ON = cos(MON)*OM.
5
Returning to the geometric definition of the tangent (tg(MON) = MN/ON), substitute the above expression. Then:
tg(MON) = sin(MON)*OM/cos(MON)*OM cut OM, then tg(MON) = sin(MON)/cos(MON).
How to find the tangent if we know the <b>cos</b>
6
From the basic trigonometric identities (sin^2(x)+cos^2(x)=1) Express the cosine, using the sine: cos(x)=(1-sin^2(x))^0,5 Substitute the expression obtained in step 5. Then tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
7
Sometimes there is a need to calculate the tangent double-angle and half-hearted. Here, too, relations are derived:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
8
It is also possible to Express the square of the tangent of a double angle cosineand or sine. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).