Instruction
1
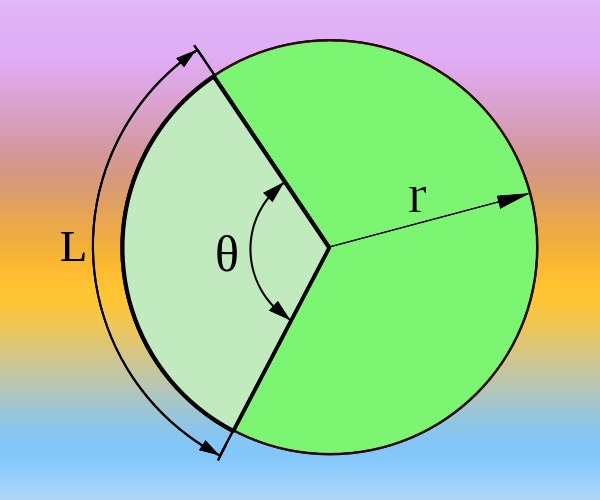
If you know the radius (R) of the circle and the arc length (L) corresponding to the desired angle (θ), you can calculate it as in degrees and in radians. Full circumference is defined by the formula 2*π*R and corresponds to the angle of 360° or two numbers of PI, if, instead of degrees, use radians. Therefore assume proportions 2*π*R/L = 360°/θ = 2*π/θ. Express from it the Central angle in radians θ = 2*π/(2*π*R/L) = L/R or the degree θ = 360°/(2*π*R/L) = 180*L/(π*R) and calculate the response according to the obtained formula.
2
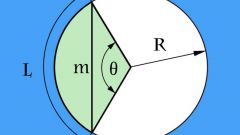
The chord length (m) connecting points of the circumference that defines a Central angle (θ), its value also can be calculated if you know the radius (R) of the circle. For this we consider the triangle formed by two radii and a chord. This is an isosceles triangle in which all parties are known, and you need to find the angle, lying opposite the base. The sine of half is equal to the ratio of the length of the base chord to twice the length of the side of the radius. So use for computing the inverse sine function the inverse sine: θ = 2*arcsin(½*m/R).
3
Knowledge of area of sector of a circle (S) bounded by radius (R) Central angle (θ) and the arc of a circle will also allow you to calculate the value of this angle. To do this, double the ratio between area and squared the radius: θ = 2*S/R2.
4
The Central angle can be specified and in the proportions of full turns or straight angle. For example, if you want to find the Central angle corresponding to a quarter of the total turnover, divide 360° into four elements: θ = 360°/4 = 90°. This value in radians needs to be equal to 2*π/4 ≈ 3,14/2 ≈ 1,57. A straight angle is equal to half of a full revolution, so, for example, the Central angle corresponding to a quarter of it will be twice less than the calculated values in degrees and in radians.