How to find the angle knowing the cosine

Use the inverse cosine (arccosine) to find the angle at the known value of the cosine. The desired value of the arc tangent, and the angle can be found for example in "tables Bradis". Paper copies of this Handbook are available in libraries and bookstores, and e-can be found on the Internet.

Find online online calculator to calculate inverse trigonometric functions and determine with their help the desired value. To use such services much easier than to look up values in tables. In addition, they can simplify the calculations since many of these calculators allow you to compute not only single values but also to the results based on the formulas composed of several operations with the trigonometric functions.

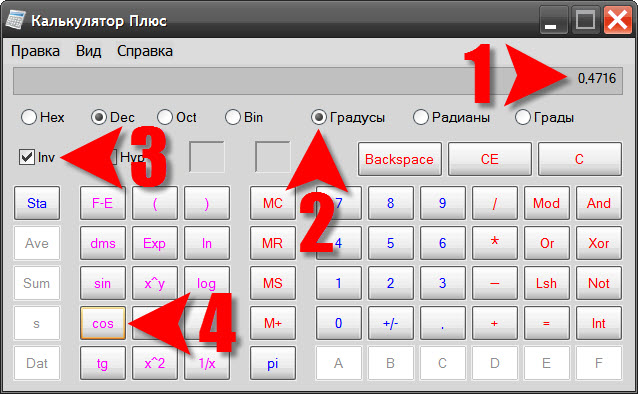
Use the standard calculator Windows, if you want to do without access to the Internet. Start command of the calculator placed in the main menu on the "start" button. Opening it, navigate to "All programs", then to "Standard" and click "Calculator". By default, it starts with the simple interface, not having tools for trigonometric calculations. Open it in menu "View" and select the item labeled "Engineering".

Enter a value for the cosineand from the keyboard, or clicking corresponding buttons of the calculator interface. Can be used to input a copy operation (CTRL + C) and paste (CTRL + V). Then select the units which should be represented the result (degrees, radians, or grads) - the corresponding selector is a line below the input field number. After this it is necessary to mark invert functions in the Inv checkbox. That's all cooking is over, click the cos and the calculator will calculate the value of the inverse cosinefunction (arccosine) of the given value and present the result in the selected units.