Instruction
1
First, according to the formula S= 180⁰(n-2) calculate the sum of the interior angles of your polygon. For example, if you need to find the angles of the right polygon with 15 sides, substitute n=15 into the equation. You get S=180⁰(15-2), S=180⁰х13, S=2340⁰.
2
Next, divide the sum of the interior angles on their number. For example, in the example of a polygon the number of corners is equal to the number of sides, i.e., 15. So, you get that the angle is 2340⁰/15=156⁰. Each interior angle of a polygon is equal to 156⁰.
3
If you prefer to calculate the angles of the polygon in radians, proceed as follows. Subtract the number of sides the number 2 and multiply the resulting difference by the number P (PI). Then divide the product by the number of angles in the polygon. For example, if you need to calculate the angles correct 15-gon, proceed as follows: C*(15-2)/15=13/15P, or to 0.87, P, or of 2.72 (but, as a rule, the number N remains unchanged). Or just divide the size of the angle in degrees by 57.3 is the number of degrees contained in one radian.
4
Can also try to calculate the angles of the right polygon, in gradians. To do this, subtract the number of sides by the number 2, divide the resulting number by the number of sides and multiply the result by 200. This unit of measurement of angles today, almost not used, but if you wanted to calculate the angles in grads, don't forget that hail is broken down into metric seconds and minutes (100 seconds in a minute).
5
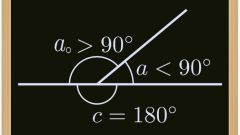
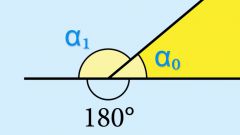
You may need to calculate the right outer angle of the polygon, in this case, act like it. Subtract from 180⁰ interior angle – the result is that you will get the value of adjacent, that is, the outer corner. It can take values from -180⁰ to +180⁰.
Useful advice
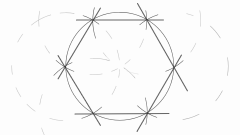
If you managed to find the corners of a regular polygon – you will be able to build it. Draw one side of a certain length and it with the protractor set aside the right angle. Measure the same distance (all the sides of a regular polygon are equal) again, put the desired angle. Continue until the sides are pinched.