Instruction
1
Use the inverse sine to calculate the angle in degrees, if you know the sine of this angle. If the angle denoted by the letter α, in General form, this can be written as: α = arcsin(sin(α)).
2
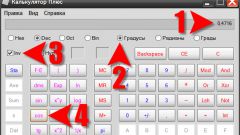
If you have the ability to use the computer for practical calculations it is easiest to use the built in calculator operating system. In the last two versions of Windows it can be run like this: press the Windows key, type the letters "ka" and press Enter. In earlier releases of this OS the link "Calculator" look at the subsection "Standard" under "All programs" in the main menu system.
3
After starting the application, switch to a mode that allows you to work with trigonometric functions. You can do this by selecting the string "Engineering" in the "View" menu of the calculator or by pressing Alt + 2.
4
Enter the value of the sine. By default, the calculator interface is no button to calculate the inverse sine. To be able to use this feature, you need to invert the values of the default button - click on the Inv button in the program window. In earlier versions, this button replaces the checkbox with the same name - put a checkmark.
5
Click on the button calculate sine - inverting functions symbol will change to sin⁻1. The calculator will calculate the angle and display its value.
6
Can be used in the calculations, and various online services, which is more than enough on the Internet. For example, go to the page http://planetcalc.com/326/, scroll it down a bit and in the Input field enter the value of the sine. To start the calculation procedure here is the orange button labeled Calculate - click it. The result of the calculation you will find in the first row of the table under this button. In addition to the arcsine and it displays the value of the arc cosine, arc tangent and arc cotangent of the entered value.