How to find the sine of the angle sides of the triangle

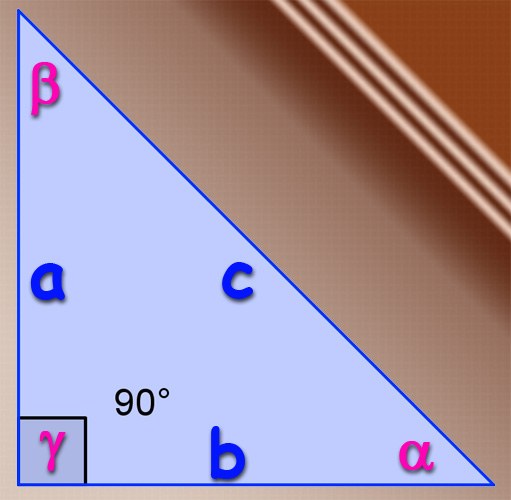
If the triangle is rectangular, then you can use the basic definition of the trigonometric functions of sine for acute angles. By definition the sine of an angle is called the ratio of length of the side lying opposite the angle to the length of the hypotenuse of this triangle. That is, if the legs have length A and b and the length of the hypotenuse is equal to C, the sine of the angle α lying opposite the side And, define by the formula α=A/C, and the sine of the angle β, which lies opposite the leg In the following formula: β=V/C. the Sine of the third angle in a right triangle to find there is no need, as the angle lying opposite the hypotenuse is always equal to 90°, and its sine is always equal to one.

For finding the sines of the angles in an arbitrary triangle, oddly enough, is easier to use the theorem of sinuses, theorem of cosines. It States that the squared length of any side is equal to the sum of the squares of the lengths of two other parties without twice the product of these lengths, the cosine of the angle between them: A2=B2+C2-2*B*C*cos(α). From this theorem we can deduce the formula for finding the cosine: cos(α)=(B2+C2-A2)/(2**). And since the sum of the squares of the sine and cosine of the same angle is always equal to unity, we can deduce the formula for finding the sine of the angle α: sin(α)=√(1-(cos(α))2)= √(1-(B2+C2-A2)2/(2**) 2).

Use for finding the sine of an angle in two different formulas for calculating the area of a triangle, one involving only the lengths of its sides and the other with the lengths of two sides and the sine of the angle between them. Since the results are equal, then from the identity we can Express the sine of an angle. The formula for finding the area using the side lengths (Heron's formula) is: S=¼*√((A+b+C)*(b+C-A)*(A+C)*(A+b-C)). And the second formula can be written as: S=A*B*sin(γ). Substitute the first equation in the second and find a formula for the sine of the angle lying opposite the side C: sin(γ)= ¼*√((A+b+C)*(b+C-A)*(A+C)*(A+b-C)/(A*)). The sinuses of the other two angles can be found in similar formulas.