Instruction
1
The triangle is rectangular if it has the right angle. In the measurement of its angles, you can use trigonometric calculations.
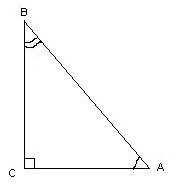
In this triangle the angle ∠C = 90º, as a direct, knowing the lengths of the sides of a triangle, the angles ∠A and ∠B are computed by the formulas: cos∠A = AC/AB cos∠B = BC/AB. Degree measures of the angles can be found by referring to the table of cosines.
In this triangle the angle ∠C = 90º, as a direct, knowing the lengths of the sides of a triangle, the angles ∠A and ∠B are computed by the formulas: cos∠A = AC/AB cos∠B = BC/AB. Degree measures of the angles can be found by referring to the table of cosines.
2
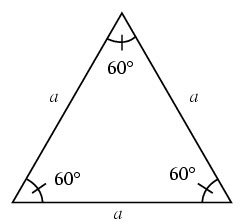
The triangle is called equilateral if all the sides are equal.
In an equilateral triangle all the angles are equal to 60º.
In an equilateral triangle all the angles are equal to 60º.
3
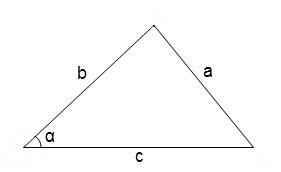
In the General case, for finding the angles in an arbitrary triangle we can use the theorem of cosines
cos∠α = (b2 + c2 - a2) / 2 • b • c
Degree measure of an angle can be found by referring to the table of cosines.
cos∠α = (b2 + c2 - a2) / 2 • b • c
Degree measure of an angle can be found by referring to the table of cosines.
4
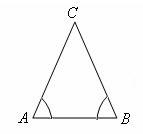
A triangle is called isosceles if two sides are equal, the third side is called the base of the triangle.
In an isosceles triangle the angles at the base are equal, i.e. ∠A = ∠B. One of the properties of a triangle is that the sum of its angles always equals 180º, so calculating the cosine theorem, the angle ∠C, the angles ∠A and ∠B we can calculate: ∠A = ∠B = 180º - ∠C)/2
In an isosceles triangle the angles at the base are equal, i.e. ∠A = ∠B. One of the properties of a triangle is that the sum of its angles always equals 180º, so calculating the cosine theorem, the angle ∠C, the angles ∠A and ∠B we can calculate: ∠A = ∠B = 180º - ∠C)/2