How to find the tangent of an angle

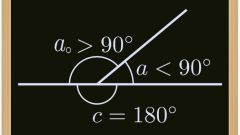
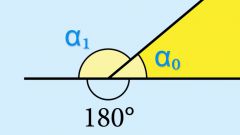
If you need to calculate the angle of inclination of a straight line to the x-axis, and you don't know the equation of the line, omit from any point of the line (except the point of intersection with the axis) perpendicular to the axis. Then measure the other two sides received a right triangle and find the ratio of adjacent side to the opposite. The resulting number will be equal to the tangent of the angle of inclination. This method is useful not only to explore the angle of inclination of a straight line, but also to measure any angles, as in the drawing, and in life (for example, the angle of the slope of the roof).

If you know the equation of the line and you need to find the tangent of the angle of inclination of this straight line to the x-axis, Express through H. as a result, you will get an expression of type y=KX+b. Note the k-factor is the tangent of the angle of inclination between the positive direction of x-axis and the beam direct located need this axis. If k=0, the tangent is also zero, then there is a direct parallel to or coincides with the abscissa axis.

If you are given a complicated function such as a quadratic, and you need to find the tangent of the angle of inclination of the tangent to this function, or, in other words, the angle coefficient, and calculate the derivative. Then calculate the value of the derivative at a given point, which will be held tangent. The resulting number is the tangent of the angle of inclination of the tangent. For example, you are given the function y=x^2+3x, the derivative, you will get an expression y`=2x+3. To find the slope at x=3, substitute this value into the equation. As a result of simple calculations it is easy to obtain y=2*3+3=9, this is the desired tangent.

To find the tangent of the angle of inclination of one side of the triangle to another, proceed as follows. Find the sine (sin) of that angle and divide it by the cosine (cos), you get the tangent of that angle.