Instruction
1
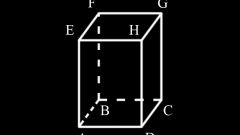
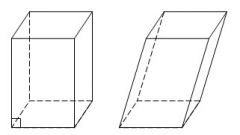
In any prism the lateral edges are at an angle to the plane of the base. A special case is a straight prism. Her sides lie in planes perpendicular to the bases. In straight prism lateral faces rectangles and the side edges equal to the height of the prism.
2
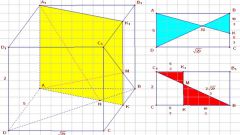
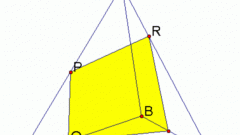
The diagonal section of the prism — part of the plane completely enclosed in the inner space of the polyhedron. Diagonal cross section can be limited by two side edges and a geometric body diagonals of the bases. It is obvious that the number of possible diagonal sections is determined by the number of diagonals in a polygon base.
3
Or borders of a diagonal cross-section can serve as the diagonal side faces and the opposite side of the bases of the prism. Diagonal cross section of a rectangular prism is a rectangle. In the General case of an arbitrary prism form a diagonal of the cross section is a parallelogram.
4
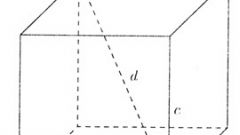
In a rectangular prism of square cross-section diagonal of S is defined by the formula:
S=d*H
where d is the diagonal of the base,
H — the height of the prism.
Or S=a*D
where a — side of the base, at the same time belonging to the cutting plane
D — the diagonal of the side face.
S=d*H
where d is the diagonal of the base,
H — the height of the prism.
Or S=a*D
where a — side of the base, at the same time belonging to the cutting plane
D — the diagonal of the side face.
5
In the random indirect prism diagonal cross section is a parallelogram, one side of which is equal to a lateral edge of the prism, the other diagonal of the base. Or sides, diagonal lines can be diagonal side faces and the sides of the bases between the vertices of the prism, where the drawn diagonal side surfaces. The area of a parallelogram S is determined by the formula:
S=d*h
where d is the diagonal of the base of the prism,
h — the height of a parallelogram — diagonal cross-section of the prism.
Or S=a*h
where a — side of the base of the prism, which is the border of the diagonal lines,
h — the height of the parallelogram.
S=d*h
where d is the diagonal of the base of the prism,
h — the height of a parallelogram — diagonal cross-section of the prism.
Or S=a*h
where a — side of the base of the prism, which is the border of the diagonal lines,
h — the height of the parallelogram.
6
To determine the height of the diagonal section is not enough to know the linear dimensions of the prism. The necessary data about the inclination of the prism to the plane of the base. A further problem is reduced to the consecutive solution of several triangles depending on the source of data on the angles between the elements of prism.