How to find the area of a rectangular prism

To start, determine what kind of shape is the base of the prism. If the base of the prism is, for example, triangle then it is called triangular, if the quadrangle - quadrilateral, Pentagon - pentagonal, etc. Since the condition indicates that the prism is rectangular, and therefore, its bases are rectangles. Prism can be straight or curved. Because the condition does not specify the angle of inclination of the side faces to the base, it can be concluded that it is straight and the lateral faces are also rectangles.

To find the area of the surface of the prism, you must know the height and the size of the sides of the base. Since the prism is straight, its height coincides with the side edge.

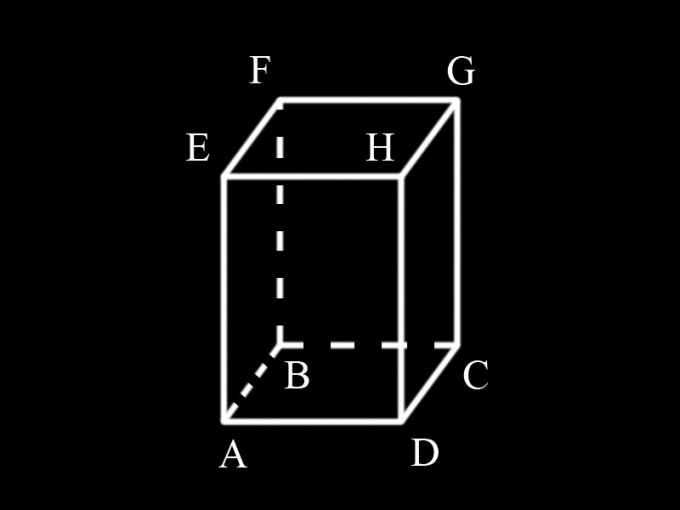
Type designation: AD = a; AB = b; AM = h; S1 – area of the bases of the prism, S2 the area of its lateral surface, S – the total area of the surface of the prism.

Base - a rectangle. The area of a rectangle is defined as the product of the lengths of its sides AB. Prism has two equal base. Hence, their total area is equal to: S1= 2ab

Prism has 4 lateral faces are rectangles. Side AD faces ADHE is both side of the base ABCD is equal. Side AE is an edge of the prism and is equal to h. The area of the face equals АЕHD a. Because the face AEHD is equal to the face BFGC, their total area: 2ah.

Face AEFB AE has an edge that is party to the bases and equal to b. Another edge is the height of the prism and is equal to h. The area of the face is equal to bh. Face AEFB is equal to the face DHGC. Their total area is equal to: 2bh.

The area of the whole lateral surface of the prism: S2 = 2ah+2bh.

Thus, the area of the surface of the prism is equal to the sum of the areas of the two bases and four lateral faces: 2ab + 2ah + 2bh or 2(ab + ah + bh). The problem is solved.