Instruction
1
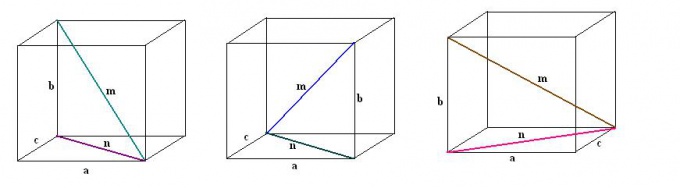
Draw a rectangular parallelepiped. Write known data: three edges a, b, C. First, build a single diagonal m. For its determination we use the property of a rectangular parallelepiped, according to which all the corners are straight.
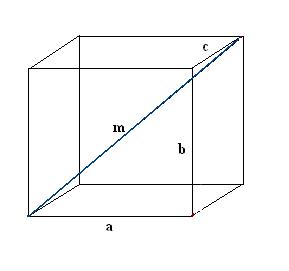
2
Construct a diagonal n one of the faces of the parallelepiped. Build a guide so that the edge is known, the required diagonal of the parallelepiped and the diagonal faces together formed a right triangle a, n, m.
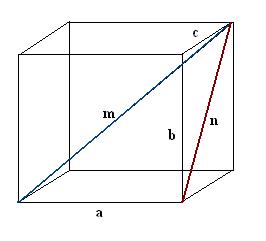
3
Find built diagonal faces. It is the hypotenuse of another right triangle b, C, n. According to the Pythagorean theorem n2 = S2 + b2. Calculate this expression and take the square root of the obtained values, it will be the diagonal of n faces.
4
Find the diagonal of a parallelepiped m. To do this in a right triangle a, n, m find the unknown hypotenuse: m2 = n2 + a2. Substitute known values, then calculate the square root. The result is the diagonal of a parallelepiped m.
5
Likewise consistently spend the remaining three diagonals of a parallelepiped. Also, for each of them will complete additional construction of the diagonals of the adjacent faces. Formed by considering right triangles and applying the Pythagorean theorem, find the values of the remaining diagonals of a rectangular parallelepiped.