How to find the area of the face of the box

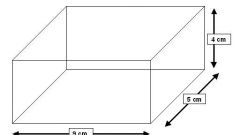
Draw a box using the pencil and ruler, placing the base horizontally. This is a classic form of representation of shapes, which can be used to demonstrate all the conditions of the problem. Then to solve it will be much easier.

Look at the picture. Have a box of six pairs of parallel faces. Each pair represents an equal two-dimensional shapes, which in General case are parallelograms. Accordingly, their areas are also equal. Thus, the total surface is the sum of the three matching variables: square of the top or bottom of the base, the front or rear faces, right, or left face.

To find the square faces of a parallelepiped, we need to consider it as a separate figure with two dimensions, length and width. At the well-known formula area of a parallelogram equals the base to the height.

The direct box only the bases are parallelograms, all the lateral faces are rectangular in shape. The area of this figure is obtained by multiplying the length by the width, since it coincides with the height. In addition, there exists a rectangular parallelepiped, all faces of which – rectangles.

The cube is also a parallelepiped, which has the unique property – equality of all measurements and the numerical characteristics of the faces. The area of each of its sides are equal to the squared length of any edge, and the full surface is obtained by multiplying this value by 6.

The form of a parallelepiped with square corners can often be found in everyday life, for example, in the construction of houses, construction of items of furniture, household appliances, toys, stationery, etc.

Example: find the area of each lateral face direct of the box, if you know that the height is 3 cm, the perimeter of the base is 24 cm and base length greater than width 2 cm Solution.Write down the formula for perimeter of parallelogram P = 2•a + 2•b. The statement b = a + 2 therefore P = 4•a + 4 = 24, whence a = 5, b = 7.

Find the area of the lateral faces of the figure with 5 sides and 3 cm rectangle:Ѕб1 = 5•3 = 15 (cm2).The area of parallel side faces, by definition of the box, also equal to 15 cm2. It remains to determine the area of the other pairs of sides with the sides 7 and 3:Ѕб2 = 3•7 = 21 (cm2).