You will need
- Knowledge of the lengths of all sides of a parallelogram.
Instruction
1
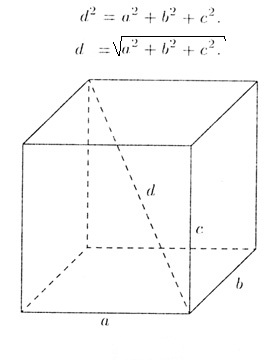
Method 1. Given a rectangular parallelepiped with sides a, b, c and diagonal d. According to one of the properties of a parallelogram, the square of the diagonal is equal to the sum of the squares of its three sides. It follows that the length of the diagonal can be calculated by extracting the square of this amount (Fig.1).
2
Method 2. Suppose a rectangular parallelepiped is a cube. Cube - is a cuboid whose each face is represented by a square. Consequently, all its sides are equal. Then the formula to calculate the length of its diagonal is expressed as:
d = a*√3
d = a*√3