Instruction
1
To find the diagonal right prism you need to understand just a few definitions.

A prism is called a polyhedron, having as bases two equal polygon (triangle, quadrangle, etc.) lying in parallel planes and the lateral faces parallelograms.
Direct the prism is called prism, whose lateral faces rectangles.
A right prism is called a straight prism, the base of which are regular polygon (equilateral triangle, square, etc.)
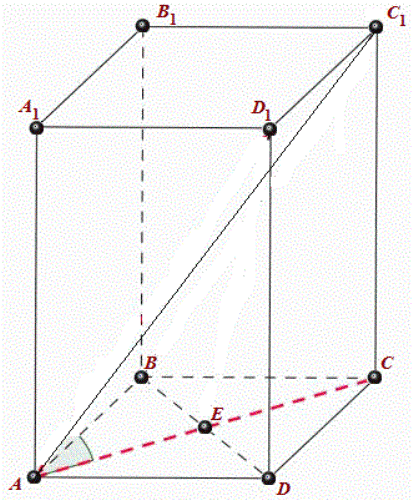
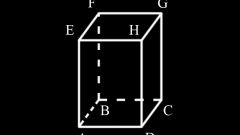
АВСDА1В1С1D1 - regular quadrangular prism.
АА1В1В - the side faces of the regular quadrangular prism.
All four side faces of the prism are equal.
ABCD and А1В1С1D1 -base of the prism (squares lying in parallel planes).
A diagonal of a polyhedron is the line segment joining two not adjacent vertices, i.e. vertices that do not belong to the same face.
The figure shows that the point A and the point 1 does not belong to one face and therefore the cut of AC1 - diagonal of the prism.
2
To find the diagonal of prism necessary to consider the triangle АСС1. This triangle is rectangular. Diagonal prism AC1 in the triangle will be the hypotenuse, and the segments as SS1 and the other two sides. From the Pythagorean theorem (in a right triangle the hypotenuse squared is equal to the sum of the squares of the legs) it follows that:
АС12 = AC2 + СС12 (1);
3
Next, you should consider the triangle АСD. Triangle АСD is also rectangular (because the base of the prism is square). For convenience, you can designate the base of the letter. Therefore, by the Pythagorean theorem:
AC2 = A2 +A2 AC = √2A (2);
4
If we denote the height of the prism with the letter h, and substitute the expression (2) into the expression (1), we get:
АС12 = 2A2+h2, AC1 = √(2a^2+h^2 ), where a - side of the base, h is the height.
This formula is valid for any right prism.