You will need
  • calculator;
  • - source data.
Instruction
1
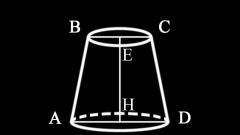
To find the area of the cross section of a parallelogram, you need to know its base and height. If, for example, are known only to the length and width of the base, find the diagonal using the Pythagorean theorem (the square of the length of the hypotenuse in a right triangle is equal to the sum of the squares of the other two sides: a2 + b2 = c2). Therefore, c = sqrt (a2 + b2).
2
Finding the value of the diagonal, substitute it in the formula S= c*h, where h is the height of the parallelogram. The result will be the largest cross-sectional area of the parallelogram.
3
If the section passes along the two grounds, the area count under the formula: S=a*b.
4
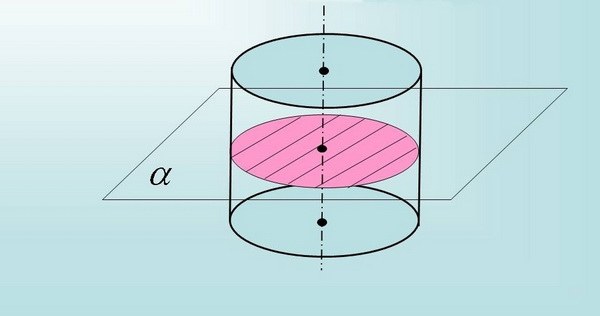
To compute the area of an axial section of the cylinder extending perpendicular to the bases (assuming that one side of this rectangle is equal to the radius of the base, and the second the height of the cylinder), use the formula S =2R*h, where R is the radius of the circle (base), S is the cross – sectional area, and h is the height of the cylinder.
5
If the conditions of the problem the section does not pass through the axis of rotation of the cylinder, but parallel to its bases, then the side of the rectangle is equal to the diameter of the circular base.
6
Independently calculate an unknown side by building a circular base of the cylinder, the conduct of the perpendiculars from the sides of the rectangle (the image plane) to the circumference and calculate the size of the chord (the Pythagorean theorem). Then substitute in S =2A*h the value obtained (2A – value of the chord) and calculate the cross-sectional area.
7
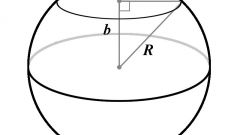
The cross-sectional area of the ball is determined by the formula S = πR2. Please note that if the distance from the center of the geometric figure to the plane will coincide with the plane of the cross-sectional area will be equal to zero, because the ball touches the plane only at one point.