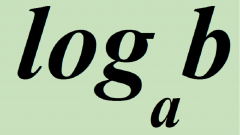You will need
- You need to know the properties of logarithms.
Instruction
1
Suppose you have a sum of two logarithms: the logarithm of the number b for the base a is loga(b), and the logarithm of the number d on the basis of the number of c – logc(d). This amount is written as loga(b) + logc(d).
You may find the following solution to this problem. First, let's see whether the trivial case when the same and the base of the logarithms (a = c), and the number under the sign of the logarithm (b = d). In this case, the logarithms of the fold as a regular number or unknown. For example, x + 5 * x = 6 * x. For logarithms: 2 * log 2(8) + 3 * log 2(8) = 5 * log 2(8).
You may find the following solution to this problem. First, let's see whether the trivial case when the same and the base of the logarithms (a = c), and the number under the sign of the logarithm (b = d). In this case, the logarithms of the fold as a regular number or unknown. For example, x + 5 * x = 6 * x. For logarithms: 2 * log 2(8) + 3 * log 2(8) = 5 * log 2(8).
2
Next, check to see if it will work is elementary to compute the logarithm. For example, as in the following example: log 2(8) + log 5(25). Here the first logarithm is calculated as log 2(8) = log 2(2^3). I.e. to what degree it is necessary to raise the number 2 to get the number 8 = 2^3. The answer is obvious: 3. Similarly, with the following logarithm: log 5 (25) = log 5 (5^2) = 2. Thus, you will receive the sum of two natural numbers: log 2(8) + log 5(25) = 3 + 2 = 5.
3
If the base of the logarithms are equal, it is in effect a property of logarithms, known as the "log of work". According to this property the sum of logarithms with same bases is equal to the logarithm of a product: loga(b) + loga(c) = loga(bc). For example, given the amount of log 4(3) + log 4(5) = log 4(3 * 5) = log 4(15).
4
If the base of the logarithms of the sum satisfy the following expression a = c^n, you can use a property of logarithm with base a power: log a^k(b) = 1/k * log a(b). For the amount of log a(b) + log c(d) = log^n(b) + log c(d) = 1/n * log c(b) + log c(d). Therefore, the logarithms are reduced to common basis. Now you need to get rid of the factor 1/n in front of the first logarithm.
To do this, use a property of the logarithm of the power: log a(b^p) = p * log a(b). For this example, it turns out that 1/n log c(b) = log c(b^(1/n)). Next is the multiplication property of logarithms works. 1/n * log c(b) + log c(d) = log c(b^(1/n)) + log c(d) = log c(b^(1/n) * d).
To do this, use a property of the logarithm of the power: log a(b^p) = p * log a(b). For this example, it turns out that 1/n log c(b) = log c(b^(1/n)). Next is the multiplication property of logarithms works. 1/n * log c(b) + log c(d) = log c(b^(1/n)) + log c(d) = log c(b^(1/n) * d).
5
Use the following example for clarity. log 4(64) + log 2(8) = log 2^(1/2) (64) + log 2(8) = 1/2 log 2(64) + log 2 (8) = log 2 (64^(1/2)) + log 2(8) = log 2 (64^(1/2) * 8) = log 2 (64) = 6.
As this example is easy to calculate, check the results: log 4(64) + log 2(8) = 3 + 3 = 6.
As this example is easy to calculate, check the results: log 4(64) + log 2(8) = 3 + 3 = 6.
Useful advice
Estimated value of the decimal logarithm (base 10) and natural logarithms (base e) can be calculated on the calculator. It is also useful to compare the result obtained by converting, with the result computed on the calculator, let and approximately, but the answers must come.