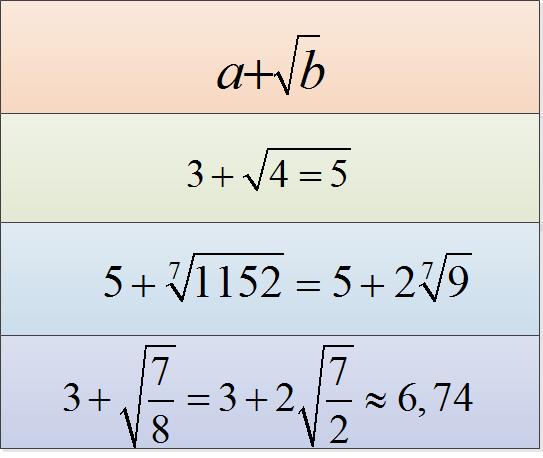Instruction
1
Let the set of expressions of the form a + √b. The first thing to do is to determine whether the number b is a perfect square. Ie try to find such a number c that c^2 = b. In this case, you extract the square root of the number b, get c and put him with number a: a + √b = a + √(c^2) = a + S. If you are not dealing with the square root, and the root of n-th degree, then complete extraction of the number b from under the sign of the root is necessary to this number was the nth degree of a certain number. For example, the number 81 will be removed from under the square root: √81 = 9. Also it will be removed from under the sign of the fourth root: (√4) 81 = 3.
2
Note the following examples.
• 7 + √25 = 7 + √(5^2) = 7 + 5 = 12. Here under the sign of the square root is the number 25, which is the full square of 5.
• 7 + (√3)27 = 7 + (√3) (3^3) = 7 + 3 = 10. Here were extracted the cube root of the number 27 which is the cube of the number 3.
• 7 + √(4/9) = 7 + √( (2/3)^2 ) = 7 + 2/3 = 23/3. To extract the square root of a fraction you must remove the root from the numerator and the denominator.
• 7 + √25 = 7 + √(5^2) = 7 + 5 = 12. Here under the sign of the square root is the number 25, which is the full square of 5.
• 7 + (√3)27 = 7 + (√3) (3^3) = 7 + 3 = 10. Here were extracted the cube root of the number 27 which is the cube of the number 3.
• 7 + √(4/9) = 7 + √( (2/3)^2 ) = 7 + 2/3 = 23/3. To extract the square root of a fraction you must remove the root from the numerator and the denominator.
3
If the b number under the root sign is not a perfect square, then try to decompose it into factors and make the multiplier, which is a complete square, under the sign of the root. Ie let the number of b has the form b = c^2 * d. Then √b = √(c^2 * d) = c * √d. Or b can contain the squares of two numbers, i.e. b = c^2 * d^2 * e * f . Then √b = √(c^2 * d^2 * e * f) = c * d * √(e * f).
4
Examples of sentencing multipliers under the sign of the root:
• 3 + √18 = 3 + √(3^2 * 2) = 3 + 3√2 = 3 * (1 + √2).
• 3 + √(7 / 4) = 3 + √ (7 / 2^2) = 3 + √7 / 2 = (6 + √7) / 2. In this example, was handed down the full square of the denominator of a fraction.
• 3 + (√4)240 = 3 + (√4) (2^4 * 3 * 5) = 3 + 2 *(√4) 15. There turned out to take 2 in the fourth degree under the sign of the fourth root.
• 3 + √18 = 3 + √(3^2 * 2) = 3 + 3√2 = 3 * (1 + √2).
• 3 + √(7 / 4) = 3 + √ (7 / 2^2) = 3 + √7 / 2 = (6 + √7) / 2. In this example, was handed down the full square of the denominator of a fraction.
• 3 + (√4)240 = 3 + (√4) (2^4 * 3 * 5) = 3 + 2 *(√4) 15. There turned out to take 2 in the fourth degree under the sign of the fourth root.
5
And finally, if you need to obtain the approximate result (if the radical expression is a perfect square), use the calculator to compute the value of the root. For example, 6 + √7 ≈ 6 + 2,6458 = 8,6458.
Useful advice
To calculate the approximate value of the root on standard calculator remember to take the square root of a number is equivalent to raising a number to the power 1/2. Similarly, the extraction of the cube root is equivalent to raising a number to the power 1/3, the fourth root – the construction of the power 1/4, etc.