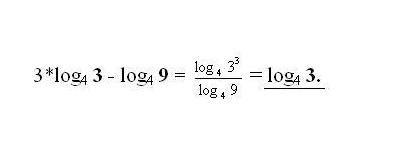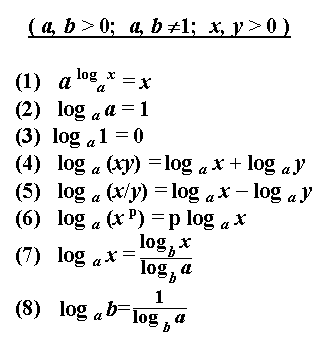Instruction
1
Write the given logarithmic expression. If the expression uses the logarithm base 10, the recording is shortened and looks: lg b is the decimal logarithm. If the logarithm is in natural base the number e, then write the expression: ln b is the natural logarithm. It is implied that the result of any logarithm is the power to which it is necessary to build a number of bases, to obtain the number b.
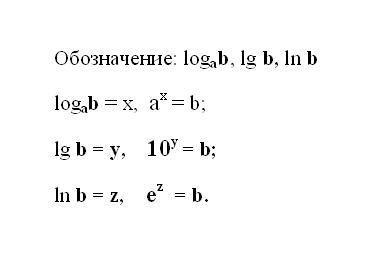
2
Solution of logarithm is calculating the relevant level. Before solving a logarithmic expression, is usually required to simplify the. Convert it using known identities, rules, and properties of the logarithm.

3
Addition and subtraction of logarithms of the numbers b and C on the same grounds is replaced by a single logarithm with a product or division of integers b and C, respectively. Apply as needed the most common transformation, the transition formula of the logarithm to another base.
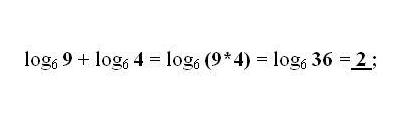
4
Using expressions to simplify a logarithm, consider the existing restrictions. So the base of the logarithm and can only be a positive number not equal to one. The number b must also be greater than zero.
5
But not always, simplifying the expression, we can calculate the logarithm to its numerical form. Sometimes it doesn't make sense, as a degree represent irrational numbers. In this case, Express the degree numbers written in the form of logarithm.